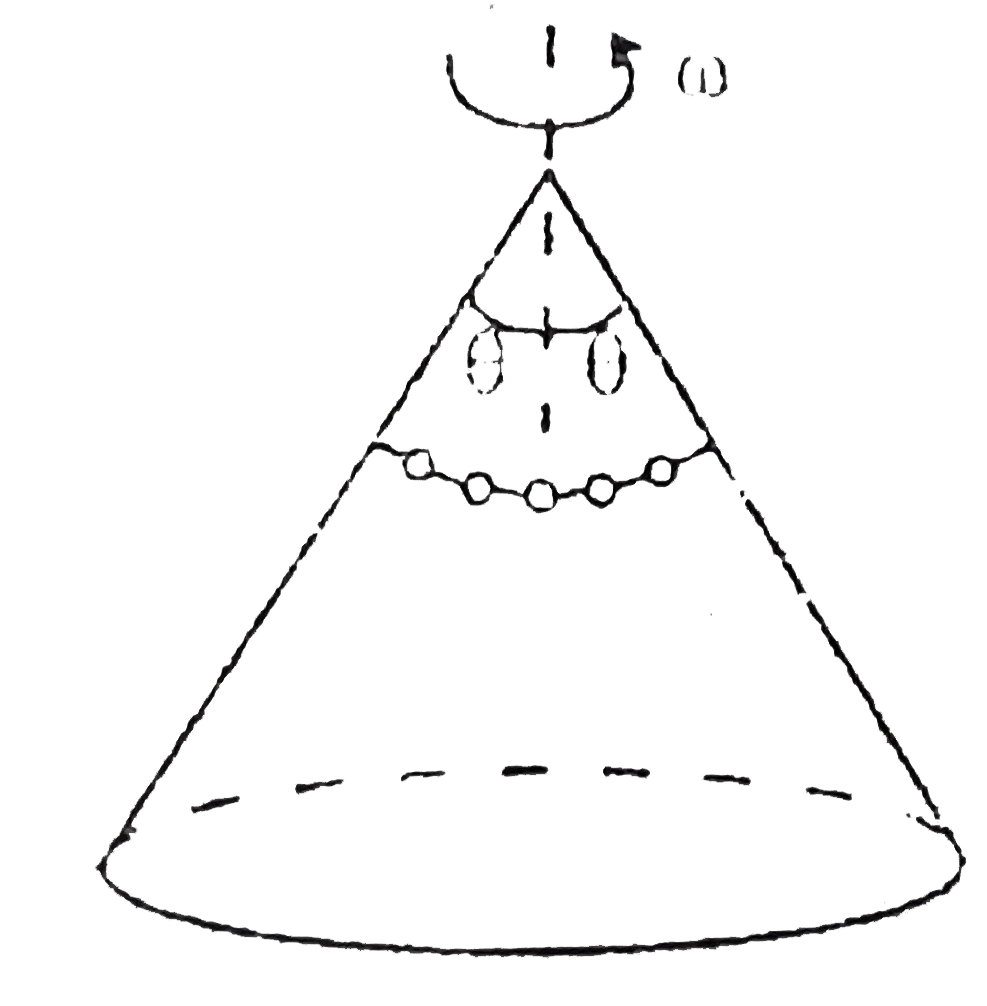
Figure-3.54(a) shows a cone of half angle θ on which a chain of mass m is resting with sufficient friction so that it will not slip on the surface of cone. If cone starts rotaring at an angular velocity ω find the tension developed in the chain.
Step by step video & image solution for Figure-3.54(a) shows a cone of half angle theta on which a chain of mass m is resting with sufficient friction so that it will not slip on the surface of cone. If cone starts rotaring at an angular velocity omega find the tension developed in the chain. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - Practice Exercise42videos
WORK, ENERGY AND POWER
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - Discussion Question31videos
WORK, ENERGY AND POWER
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Unsolved Numerical63videos
RIGID BODIES AND ROTATIONAL MOTION
Similar Questions
A chain of mass 'm' and radius 'r' is placed onto a cone of semi vertical angle θ. Cone rotated with angular velocity ω. Find the tension in the chain if it does not slide on the cone.
View Solution_S01_038_Q01.png)
As per the shown figure the central solid cylinder starts with initial angular velocity ω0 Find the time after which the angular velocity becomes half.View Solution
Knowledge Check
- Question 1 - Select One
A point mass m collides with a disc of mass m and radius R resting on a rough horizontal surface as shown . Its collision is perfectly elastic. Find angular velocity of the disc after pure rolling starts
A(2u3R)B(3u3R)C(5u3R)D(2u5R) - Question 2 - Select One
A rod AB of length l = 1m and mass m = 2kg is pinned to a vertical shaft and a massless string is tied with the shaft at the lower end of the rod ( length of the string is 45m ) as shown in figure.If the shaft starts rotating with a constant angular velocity ω=5 rad / sec. Then find the tension in the string.
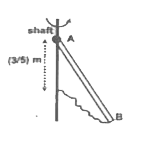A1NB2NC3ND0N - Question 3 - Select One
A block A of mass M rests on a wedge B of mass 2M and inclination θ. There is sufficient friction between A and B so that A does not slip on B. If there is no friction between B and ground, the compression in spring is
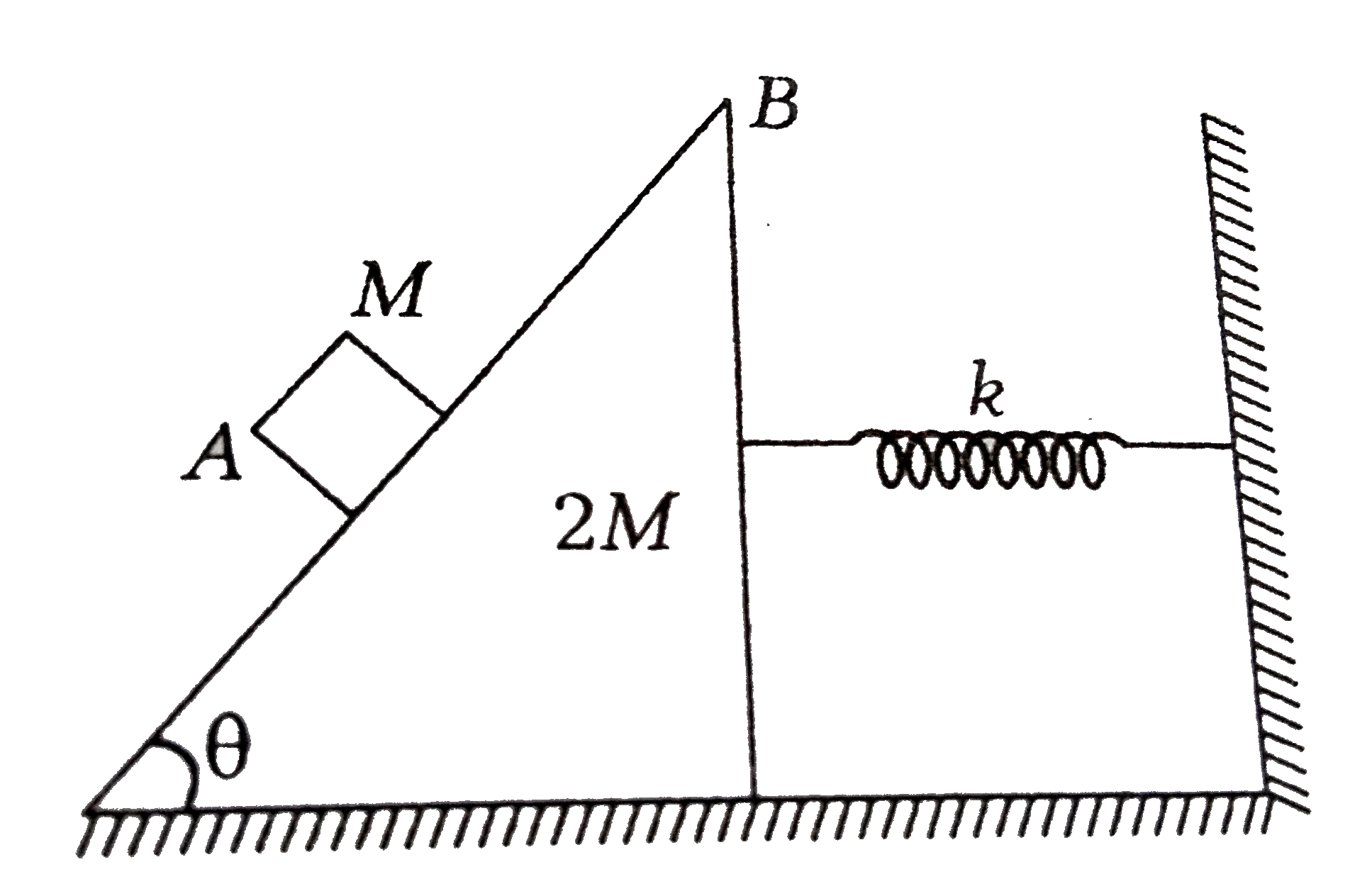AMgcosθkBMgcosθsinθkCMgsinθkDzero
A mass m is attached to a pulley through a cord as shown in figure. The pulley is a solid disk with radius R. The cord does not slip on the disk. The mass is released from rest at a height h from the ground and at the instant the mass reaches the ground, the disk is rotating with angular velocity ω. Find the mass of the disk.
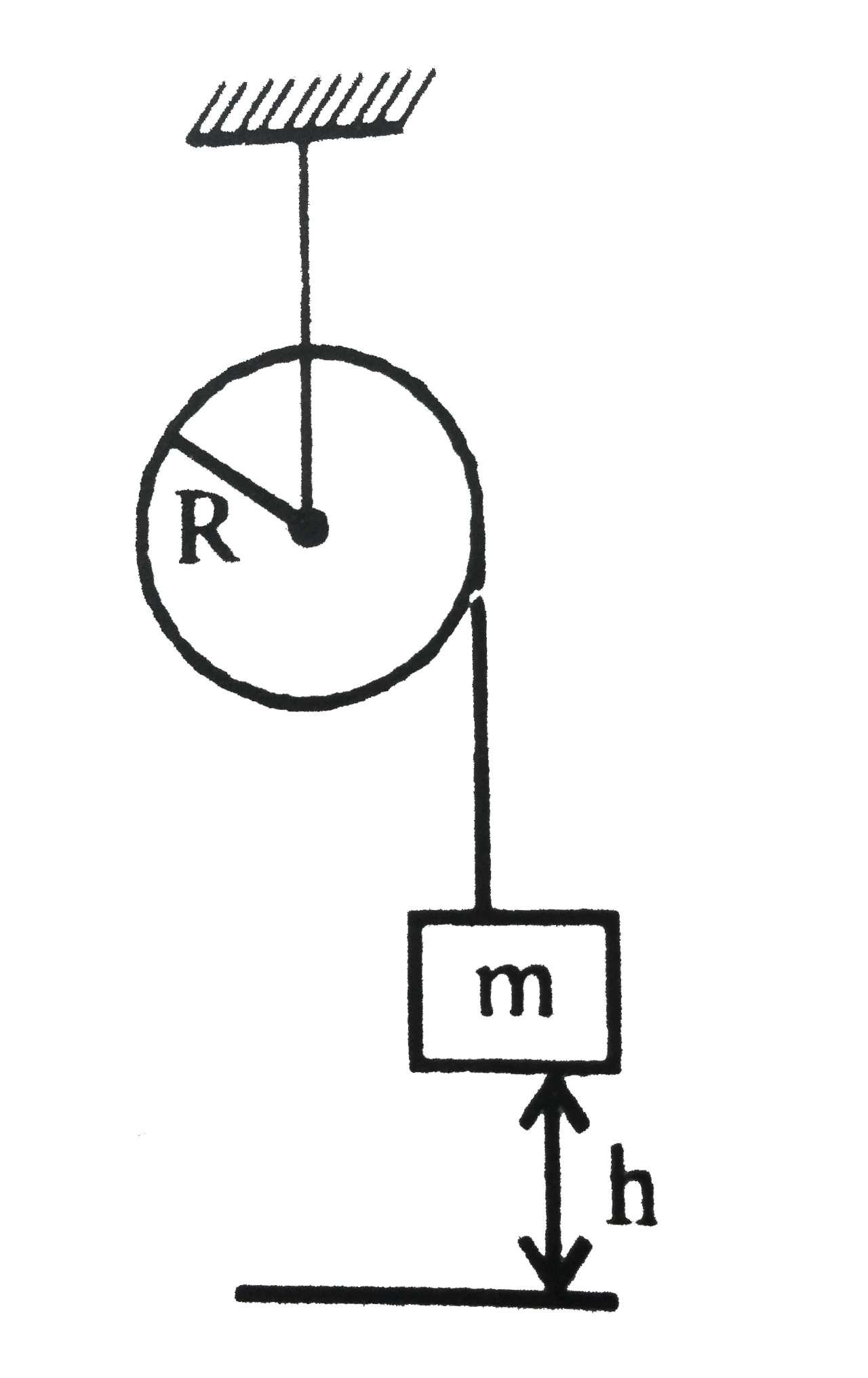.View SolutionThe coefficient of static friction between a block of mass m and an incline is μs=03, a. What can be the maximum angle θ of the incline with the horizontal so that the block does not slip on the plane? b. If the incline makes an angle θ2 with the horizontal, find the frictional force on the block.
View SolutionA uniform rod of maass m and length L is placed on the fixed cylindrical surface of radius R at an small angular position θ from the vertical (vertical means line joining centre and vertex of the cylindrical path) as shown in the figure and released from rest. Find the angular velocity ω of the rod at the instant when it crosses the horizontal position (Assume that when rod comes at horizontal position its mid point and vertex of the circular surface coincide). Friction is sufficient to prevent any slipping.
View SolutionTwo particles of mass m and 2m are connected by a string of length L and placed at rest over a smooth horizontal surface. The particles are then given velocities as indicated in the figure shown. The tension developed in the string will be
View SolutionA uniform thin rod of mass m and length l is standing on a smooth horizontal suface. A slight disturbance causes the lower end to slip on the smooth surface and the rod starts falling. Find the velocity of centre of mass of the rod at the instant when it makes an angle θ with horizontal.
View Solution