A man pulls a bucket of water from a depth of h from a well. If the mass of the rope and that of bucket full of water are m and M respectively, the work done by the man is :
(M+m)gh
(M+m2)gh
(M+m2)gh
(M2+m)gh
The correct Answer is:B
To solve the problem of calculating the work done by a man pulling a bucket of water from a depth h in a well, we can break it down into a series of steps:
1. Identify the Forces Involved:
- The man pulls a bucket of mass M and a rope of mass m.
- The gravitational force acting on the bucket is Mg (where g is the acceleration due to gravity).
- The gravitational force acting on the rope is mg.
2. Determine the Displacement:
- The bucket is pulled from a depth h to the top of the well, which means it is displaced by a distance h.
- The center of mass of the rope, which has a uniform mass distribution, is located at a height of h2 when the entire rope is pulled up.
3. Calculate Work Done on the Bucket:
- The work done Wb on the bucket can be calculated using the formula:
Wb=Force×Displacement=Mg×h
4. Calculate Work Done on the Rope:
- The work done Wr on the rope is calculated by considering the center of mass of the rope being lifted by h2:
Wr=Force×Displacement=mg×h2
5. Total Work Done by the Man:
- The total work done W by the man is the sum of the work done on the bucket and the work done on the rope:
W=Wb+Wr=Mg⋅h+mg⋅h2
6. Factor Out Common Terms:
- We can factor out gh from the total work done:
W=gh(M+m2)
Final Answer:
The work done by the man in pulling the bucket of water from a depth h is:
W=gh(M+m2)
- The man pulls a bucket of mass M and a rope of mass m.
- The gravitational force acting on the bucket is Mg (where g is the acceleration due to gravity).
- The gravitational force acting on the rope is mg.
- The bucket is pulled from a depth h to the top of the well, which means it is displaced by a distance h.
- The center of mass of the rope, which has a uniform mass distribution, is located at a height of h2 when the entire rope is pulled up.
- The work done Wb on the bucket can be calculated using the formula:
Wb=Force×Displacement=Mg×h
- The work done Wr on the rope is calculated by considering the center of mass of the rope being lifted by h2:
Wr=Force×Displacement=mg×h2
- The total work done W by the man is the sum of the work done on the bucket and the work done on the rope:
W=Wb+Wr=Mg⋅h+mg⋅h2
- We can factor out gh from the total work done:
W=gh(M+m2)
The work done by the man in pulling the bucket of water from a depth h is:
W=gh(M+m2)
Topper's Solved these Questions
- WORK, ENERGY AND POWERBook:PHYSICS GALAXY - ASHISH ARORAChapter:WORK, ENERGY AND POWERExercise:unsolvedMCQ
Explore 78 Videos
- WORK, ENERGY AND POWERBook:PHYSICS GALAXY - ASHISH ARORAChapter:WORK, ENERGY AND POWERExercise:unsolved
Explore 1 Video
- WORK, ENERGY AND POWERBook:PHYSICS GALAXY - ASHISH ARORAChapter:WORK, ENERGY AND POWERExercise:Discussion Question
Explore 31 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:RIGID BODIES AND ROTATIONAL MOTIONExercise:Unsolved Numerical
Explore 63 Videos
Similar Questions
A man slowly pulls a bucket of water from a well of depth h=20m. The mass of the uniform rope and bucket full of water are m=200g and M=19.9kg respectively. Find the work done (in kJ) by the mean.
View SolutionTrenton is pulling a bucket full of water, out of a well.
What is Trenton working against?
View Solution
Knowledge Check
A person pulls a bucket of water from a well of depth h. if the mass of uniform rope is and that of the bucket full 0f water is M, then work done by the person is.
A(M+m2)ghB1/2 (M + m)ghC(M+m)ghD(M2+m)ghA bucket full of water is drawn up by a person. In this case the work done by gravitational force is
Anegative because the force and displacement are in opposite directionsBpositive because the force and displacement are in the same directionCnegative because the force and displacement are in the same directionDpositive because the force and displacement are in opposite directionA man pulls out a block of mass m from the depth d with help of a light string. If acceleration of the block is g2 then the work done by the string on the block will be
A−3mgd2B+3mgd2C−mgd2D+mgd2
Water is lifted from a well of depth 50m .If mass of water is 20Kg and weight of the rope is 0.2Kg and per metre the amount of work done is
View SolutionA bucket is in the form of a frustum of a cone. Its depth is 15 cm and the diameters of the top and the bottom are 56 cm and 42 cm respectively. Find how many litres of water the bucket can hold. [ Take π=227].
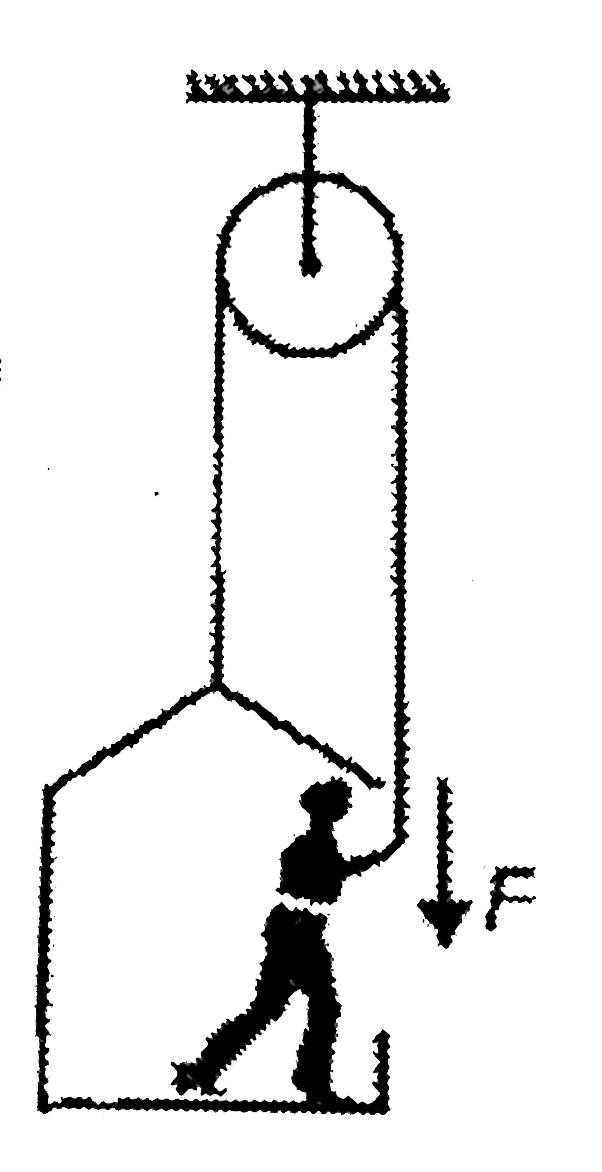
View SolutionA man of mass M stands on a.box of mass m as shown in the Fig. 2E. l (a). A rope attached to 'the box and passing over an overhead pulley allows the man to raise himself and the box by , pulling the rope downward.
(i) With what minimum force should the ' man pull the rope so as to prevent himself , from falling down.
(ii) If the man pulls the rope with a force F greater than the minimum force, then determine the acceleration of the (man + box) system.
(iii) Determine. the normal reaction between the man and the trolley.
View SolutionFind the net downward thrust on the clined surface of a bucket full of water of height h and radii a and b.
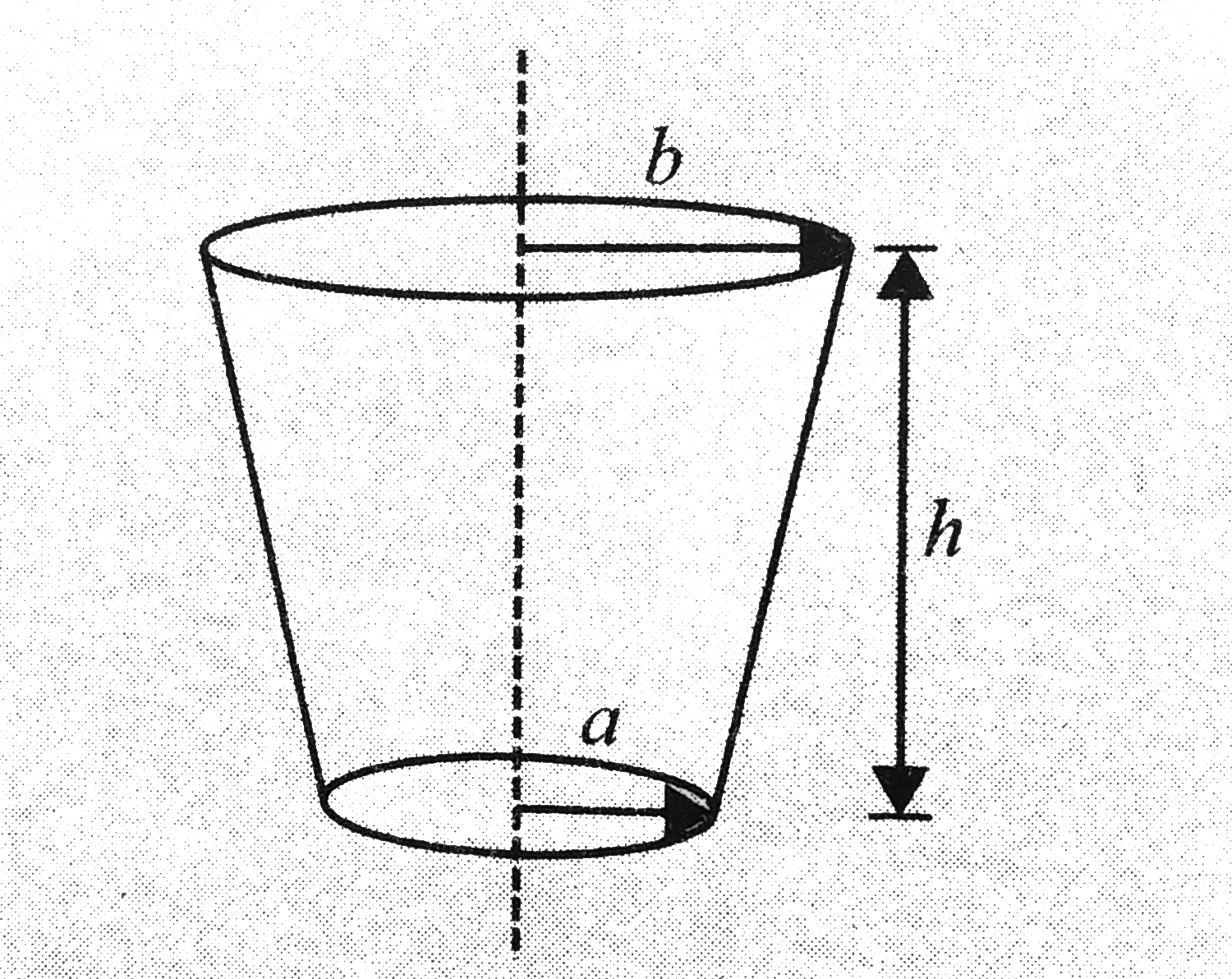
View SolutionA person holds a bucket of weight 60N . He walks 7m along the horizontal path and then climbs up a vertical distance of 5m. The work done by the man is
View Solution