A ball of mass m is attached to the lower end of a light vertical spring of force constant K. The upper end of the spring is fixed. The ball is released from rest with the spring at its normal ( unstretched ) length, and comed to rest again after descending through a distance x.
x=mg/k
x=2mg/k
The ball will have no acceleration at the position where it has descended through x/2
The ball will have an upward acceleration equal to g at its lowermost position.
The correct Answer is:B, C, D
Step by step video, text & image solution for A ball of mass m is attached to the lower end of a light vertical spring of force constant K. The upper end of the spring is fixed. The ball is released from rest with the spring at its normal ( unstretched ) length, and comed to rest again after descending through a distance x. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - unsolvedMCQ78videos
WORK, ENERGY AND POWER
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - unsolved1videos
WORK, ENERGY AND POWER
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - Discussion Question31videos
WORK, ENERGY AND POWER
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Unsolved Numerical63videos
RIGID BODIES AND ROTATIONAL MOTION
Similar Questions
A block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.
 View Solution
View SolutionA block of mass 'm' is attached to the light spring of force constant K and released when it is in its natural length. Find amplitude of subsequent oscillations.
View Solution
Knowledge Check
- Question 1 - Select One
Two blocks of masses m1 and m2 are attached to the lower end of a light vertical spring of force constant k. The upper end of the spring is fixed. When the system is in equilibrium, the lower block (m2) drops off. The other block (m1) will
 Aremain undistrubedBmove through a distance m2gk and come to restCundergo vertical SHM with a time period of 2π√m1kDundergo vertical SHM with a time period of
Aremain undistrubedBmove through a distance m2gk and come to restCundergo vertical SHM with a time period of 2π√m1kDundergo vertical SHM with a time period of
2π√m1+m2k - Question 2 - Select One or More
A mass of 0.2kg is attached to the lower end of a massless spring of force-constant 200N/m, the upper end of which is fixed to a rigid support. Which of the following statements is/are true?
AIn equilibrium, the spring will be stretched by 1cm.BIf the mass is raised till the spring is unstreched state and then released, it will godown by 2cm before moving upwards.CThe frequency of oscillation will be nearly 5Hz.DIf the system is taken to the moon, the frequency of oscillation will be the same as on the earth. - Question 3 - Select One
A particle of mass m is fixed to one end of a light spring of force constant k and unstretched length l. The other end of the spring is fixed on a vertical axis which is rotaing with an angular velocity ω. The increase in length of th espring will be
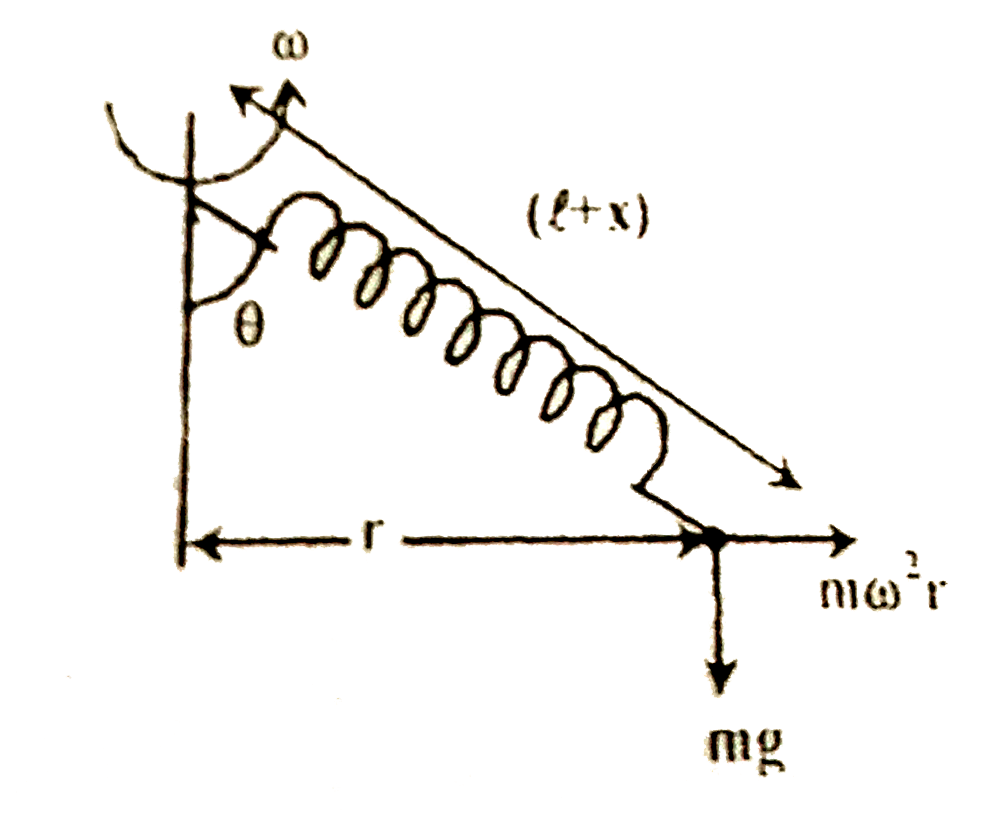 Amω2lkBmω2lk−mω2Cmω2lk+mω2DNone of these
Amω2lkBmω2lk−mω2Cmω2lk+mω2DNone of these
A block of mass m, attached to a spring of spring constant k, oscilltes on a smooth horizontal table. The other end of the spring is fixed to a wall. If it has speed v when the spring is at its naturla lenth, how far will it move on the table before coming to an instantaneous rest?
View SolutionA block of mass m attached in the lower and vertical spring The spring is hung from a calling and force constant value k The mass is released from rfest with the spring velocity unstrached The maximum value praduced in the length of the spring will be
View SolutionA block of mass m, attacted to a string of spring constant k, oscillates on a smooth horizontal table. The other end of the spring is fixed to a wall. The block has a speed v when the spring is at its natural length. Before coming to an instantaneous rest. If the block moves a distance x from the mean position, then
View SolutionA block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.
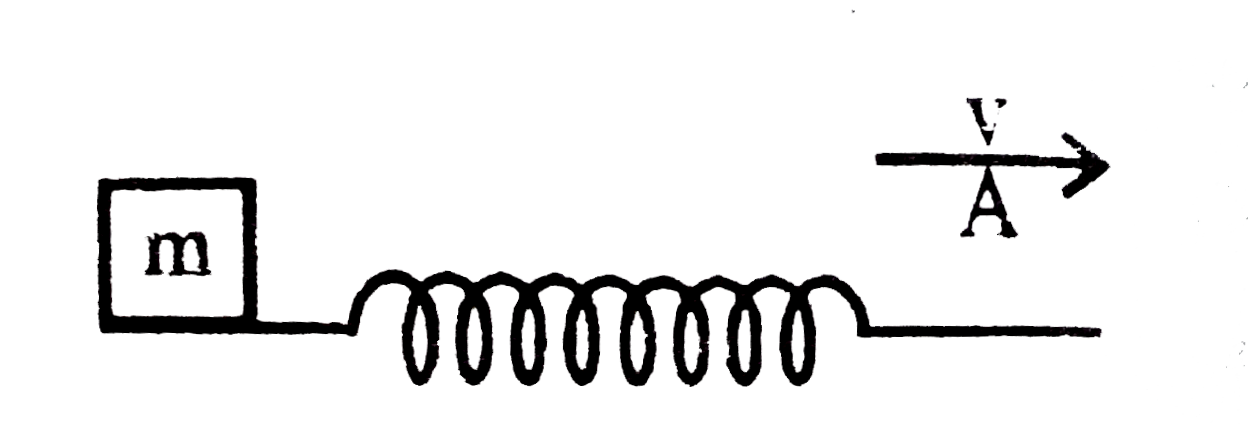 View Solution
View SolutionA Bead of mass m is attached to one end of a spring of natural length 'R' and spring cosntant 'k=(√3+1)mgR'. The other end of the spring is fixed at point 'A' on a smooth vertical ring of radius 'R' as shown
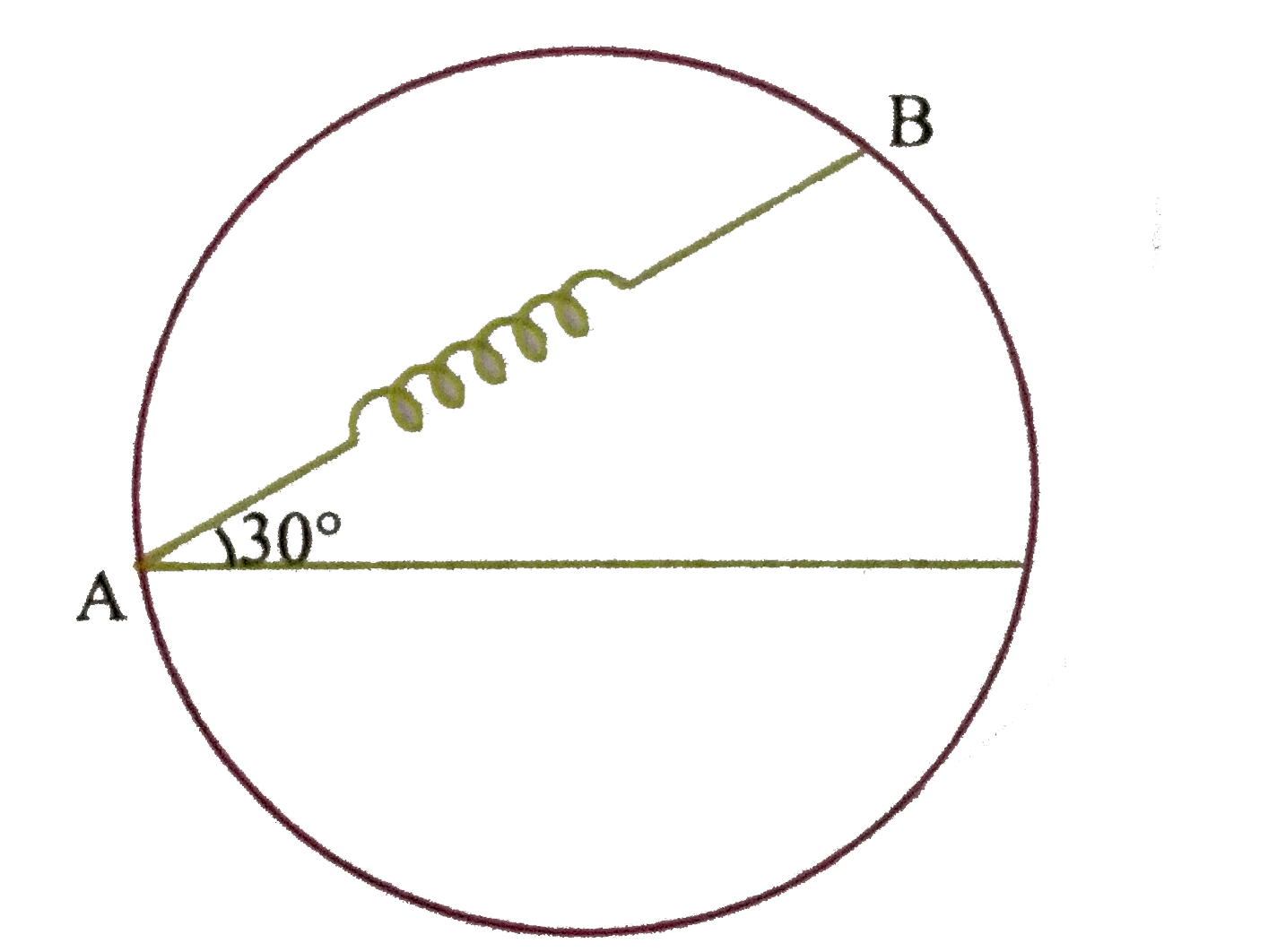 View Solution
View Solution

