A smooth table is placed horizontally and a spring of unstretched length i0 and force constank k has one end fixed to its center. To the other end of the spring is attached a mass m which is making n revolutions per second around the center. Show that the radius r of this unifrom circular motion is kl0/(k−4π2mn2) and the tension T in the spring is 4π2mkl0n2/(k−4π2mn2)
The correct Answer is:A
Step by step video, text & image solution for A smooth table is placed horizontally and a spring of unstretched length i_(0) and force constank k has one end fixed to its center. To the other end of the spring is attached a mass m which is making n revolutions per second around the center. Show that the radius r of this unifrom circular motion is kl_(0)//(k-4 pi^(2)mn^(2)) and the tension T in the spring is 4pi^(2)mkl_(0)n^(2)//(k-4pi^(2)mn^(2)) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, ENERGY AND POWERBook:PHYSICS GALAXY - ASHISH ARORAChapter:WORK, ENERGY AND POWERExercise:unsolved
Explore 1 Video
- WORK, ENERGY AND POWERBook:PHYSICS GALAXY - ASHISH ARORAChapter:WORK, ENERGY AND POWERExercise:MCQ
Explore 158 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:RIGID BODIES AND ROTATIONAL MOTIONExercise:Unsolved Numerical
Explore 63 Videos
Similar Questions
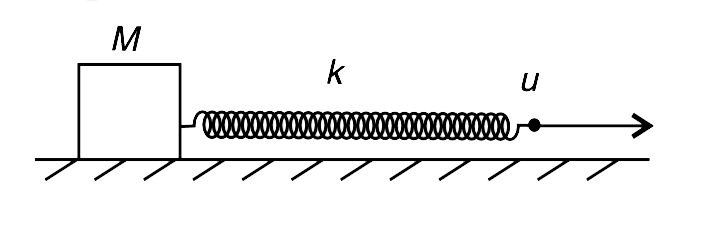
A block of mass M is placed on a horizontal smooth table. It is attached to an ideal spring of force constant k as shown. The free end of the spring is pulled at a constant speed u. Find the maximum extension (x0) in the spring during the subsequent motion.
View SolutionA spring which obeys Hooke's law extends by 1cm when a mass is hung on it.It extends by a further 3cm when the attached mass is moved in a horizontal circle making 2 revolutions per second.What is the length of the unstretched spring? Take g=π2ms−2 .
View Solution
Knowledge Check
A string of length L is fixed at one end and carries a mass M at the other end. The string makes 2/π revolution per second around the vertical axis through the fixed end as shown in the figure, then tension in the string is.
 AMLB2MLC4MLD16ML
AMLB2MLC4MLD16MLA Bead of mass m is attached to one end of a spring of natural length 'R' and spring cosntant 'k=(√3+1)mgR'. The other end of the spring is fixed at point 'A' on a smooth vertical ring of radius 'R' as shown
 AThe normal reaction at 'B' just after the bead is released to move is:3√3mg2BThe tangential acceleration of the bead just after it is released to move is :g/2CThe normal reaction at 'B' just after the bead is released to move is :3mg2DJust after the bead is released to move the normal acceleration and Tangential acceleration are numerically equal.
AThe normal reaction at 'B' just after the bead is released to move is:3√3mg2BThe tangential acceleration of the bead just after it is released to move is :g/2CThe normal reaction at 'B' just after the bead is released to move is :3mg2DJust after the bead is released to move the normal acceleration and Tangential acceleration are numerically equal.A string of length 1 m is fixed at one end and carries a mass of 100 gm at the other end. The string makes (2/π) revolutions per second around vertical axis through the fixed end. Calculate the tension in the string-
A1.0 NB1.6 NC2ND4N
A spring which obeys Hooke's law extends by 1cm when a mass is hung on it.It extends by a further 3cm when the attached mass is moved in a horizontal circle making 2 revolutions per second.What is the length of the unstretched spring? Take g= π2.
View SolutionA massless spring of natural length of 0.5 m and spring constant 50 N/m has one end fixed and the other end attached to a mass of 250 g. The spring mass system is on a smooth floor. The mass is pulled until the length of the spring is 0.6 m and then released from rest. The kinetic energy of the mass when the length of the spring is 0.5 m is
View SolutionOne end of an ideal spring of unstreched length lO=1m, is fixed on a frictionless horizontal table. The other end has a small disc of mass 0.1kg attached to it. The disc is projected with a velocity υ0=11m/s perpendicular to the spring.

What is the force constant of spring?
View SolutionA Bead of mass m is attached to one end of a spring of natural length 'R' and spring cosntant 'k=(√3+1)mgR'. The other end of the spring is fixed at point 'A' on a smooth vertical ring of radius 'R' as shown

View SolutionA bead of mass 'm' is attached to one end of a spring of natural length R & spring constant k=(√3+1)R. The other end of the spring is fixed at point A on a smooth vertical ring of radius R as shown. The normal reaction at B just after it is released to move is

View Solution