Let A,B,C be three points in a straight line. B lying between AandC. Consider all circles passing through BandC. The points of contact of the tangents from A to these circle lie on
Step by step video & image solution for Let A, B, C be three points in a straight line. B lying between A and C. Consider all circles passing through B and C. The points of contact of the tangents from A to these circle lie on by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Three circles whose radii are a,b and c and c touch one other externally and the tangents at their points of contact meet in a point. Prove that the distance of this point from either of their points of contact is (abca+b+c)12.
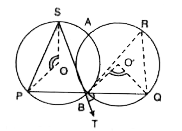
View Solutionदिए गए चित्र में दो सर्वांगसम वृत्त C(O,r) और C(O',r) जो एक दूसरे को A और B बिंदु पर प्रतिछेद करते है PBQ एक रेखा है, जो B बिंदु से गुजरती है। वृत्त C(O',r ) पर स्पर्श रेखा SBT है जो दूसरे वृत्त C को S बिंदु पर प्रतिछेद करती है, तो सिद्ध कीजिये: SP=BQ
View SolutionConsider the point A (0,0), b(4,2) and C (8,0)
Find the equation of the circum circle (Circle passing through the point A,B and C) of triangle ABC.
View SolutionConsider the points A (4,3), B (8,-3) and C (0,9)
Prove that A, B, C can't lie on a circle
View SolutionLet the midpoint of the chord of contact of tangents drawn from A to the circle x2+y2=4 be M(1,−1) and the points of contact be B and C

View SolutionThe chord of contact of tangents from 3 points A, B, C to the circle x2+y2=4 are concurrent, then the points A, B and C are:
View SolutionA circle passes through a fixed point A and cuts two perpendicular straight lines through A in B and C. If the straight line BC passes through a fixed-point (x1,y1), the locus of the centre of the circle, is
View SolutionThree circles whose radii are a,b and c and c touch one other externally and the tangents at their points of contact meet in a point. Prove that the distance of this point from either of their points of contact is (abca+b+c)12.
View Solution
