Two cells having an internal resistance of 0.2Ω and 0.4Ω are connected in parallel, the voltage across the battery is 1.5 V. If the emf of one cell is 1.2 V, then the emf of second cell is
2.1 V
2.7 V
3 V
4.2 V
The correct Answer is:A
To solve the problem, we need to find the electromotive force (emf) of the second cell when two cells with internal resistances of 0.2Ω and 0.4Ω are connected in parallel, with a voltage across the battery of 1.5V and the emf of the first cell being 1.2V.
1. Identify the known values:
- Internal resistance of the first cell, R1=0.2Ω
- Internal resistance of the second cell, R2=0.4Ω
- Voltage across the battery, V=1.5V
- Emf of the first cell, E1=1.2V
- Emf of the second cell, E2=?
2. Use the formula for voltage in parallel circuits:
The total voltage across the battery in a parallel circuit can be expressed as:
V=E1R2+E2R1R1+R2
3. Substitute the known values into the equation:
1.5=1.2×0.4+E2×0.20.2+0.4
4. Calculate the denominator:
0.2+0.4=0.6
5. Rewrite the equation:
1.5=0.48+0.2E20.6
6. Multiply both sides by 0.6 to eliminate the denominator:
1.5×0.6=0.48+0.2E2
0.9=0.48+0.2E2
7. Rearrange the equation to isolate E2:
0.2E2=0.9−0.48
0.2E2=0.42
8. Solve for E2:
E2=0.420.2=2.1V
Final Answer:
The emf of the second cell is E2=2.1V.
- Internal resistance of the first cell, R1=0.2Ω
- Internal resistance of the second cell, R2=0.4Ω
- Voltage across the battery, V=1.5V
- Emf of the first cell, E1=1.2V
- Emf of the second cell, E2=?
The total voltage across the battery in a parallel circuit can be expressed as:
V=E1R2+E2R1R1+R2
1.5=1.2×0.4+E2×0.20.2+0.4
0.2+0.4=0.6
1.5=0.48+0.2E20.6
1.5×0.6=0.48+0.2E2
0.9=0.48+0.2E2
0.2E2=0.9−0.48
0.2E2=0.42
E2=0.420.2=2.1V
The emf of the second cell is E2=2.1V.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - BITSAT GUIDECHAPTER - CURRENT ELECTRICITYEXERCISE - Bitsat Archives
26 Videos
- CATHODE RAY, PHOTOELECTRIC EFFECT AND X-RAYSBOOK - BITSAT GUIDECHAPTER - CATHODE RAY, PHOTOELECTRIC EFFECT AND X-RAYSEXERCISE - BITSAT Archives
6 Videos
- ELECTRIC CAPACITORBOOK - BITSAT GUIDECHAPTER - ELECTRIC CAPACITOREXERCISE - BITSAT archives
6 Videos
Similar Questions
Two cells of emfs 1.5 V and 2.0 V having internal resistances 0.2Ω and 0.3Ω respectively are connected in parallel. Calculate the emf and internal resistance of the equivalent cell.
View SolutionTwo cells of emfs 1.5 V and 2.0v having internal resistance 0.2Σ and 0.3 Σ respectively are connected in parallel . Calculate the emf and internal resistance of the equivalent cell .
View Solution
Knowledge Check
Two cells having the internal resistance 0.2Ωand 0.4Ωare connected in parallel. The voltage across the battery terminal is 1.5V. The emf of first cell is 1.2 V. The emf of second cell is
A2.7 VB2.1 VC3 VD4.2 VTwo cells of emf 1.25V,0.75V and each of internal resistance 1Ω are connected in parallel. The effective emf will be
A1 VB1.25 VC2 VD0.5 VA cell of emf 2 V and internal resistance 0.1Ω is connected with a resistance of 3.9Ω The voltage across the cell terminal will be
A1.95VB1.90VC0.50VD2.00V
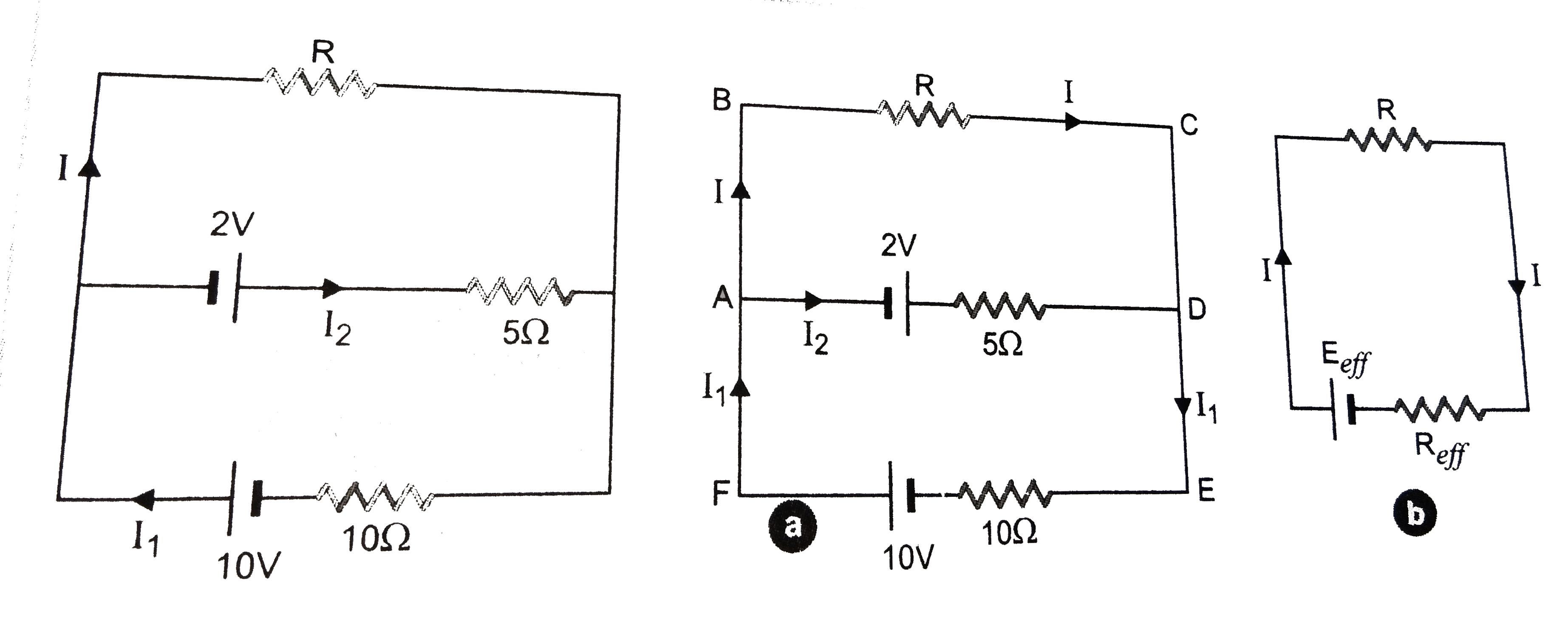
Two cells of voltage 10Vand 2V and internal resistance 10Ω and 5Ω respectively , are connected in parallel with the pesition and of 10V battery connected to negative pole of 2V battery Find the effected voltage and effected resistance of the combination
View SolutionA cell of emf 2.0 V and internal resistance 0.1 Ω is connected with a resistance of 3.9Ω. The voltage across the cell terminals will be
View SolutionTwo cells of e.m.f. 2.5 V and 2.0 V having internal resistance of 1Ω and 2Ω respectively are connected in parallel with similar poles connected together so as to send the current in the same direction through an external resistance of 2Ω. The current in the external resistance is
View SolutionThe cell has an emf of 2 V and the internal resistance of this cell is 0.1Ω, it is connected to resistance of 3.9Ω, the voltage across the cell will be
View SolutionThe cell has an emf of 2V and the internal resistance of this cell is 0.1Ω, it is connected to resistance of 3.9Ω, the voltage across the cell will be
View Solution
