A point charge Q is placed at the centre of a hemisphere. Find the electric flux passing through flat surface of hemisphere.
Qε0
Zero
Q2ε0
None of these
To solve the problem of finding the electric flux passing through the flat surface of a hemisphere with a point charge Q placed at its center, we can follow these steps:
1. Understand the Setup:
We have a point charge Q located at the center of a hemisphere. The hemisphere has a curved surface and a flat circular base.
2. Apply Gauss's Law:
Gauss's Law states that the total electric flux Φ through a closed surface is equal to the charge enclosed Qin divided by the permittivity of free space ϵ0:
Φ=Qinϵ0
3. Consider a Closed Surface:
Since the hemisphere is not a closed surface, we can imagine completing the hemisphere into a full sphere by adding an identical hemisphere. Thus, we can treat the entire sphere as a closed surface.
4. Calculate the Total Flux through the Sphere:
For the entire sphere, the charge Q is enclosed, so the total electric flux through the sphere is:
Φsphere=Qϵ0
5. Determine the Flux through the Hemisphere:
Since the flux is uniformly distributed over the entire surface of the sphere, the flux through the hemisphere (which is half of the sphere) is:
Φhemisphere=12Φsphere=12(Qϵ0)=Q2ϵ0
6. Identify the Flux through the Flat Surface:
The total flux through the hemisphere includes both the curved surface and the flat surface. However, due to symmetry, the flux through the flat surface is equal to the flux through the curved surface.
Since the total flux through the hemisphere is Q2ϵ0, and it is evenly distributed between the flat surface and the curved surface, the flux through the flat surface is:
Φflat=12Φhemisphere=12(Q2ϵ0)=Q4ϵ0
Final Answer:
The electric flux passing through the flat surface of the hemisphere is:
Φflat=Q4ϵ0
We have a point charge Q located at the center of a hemisphere. The hemisphere has a curved surface and a flat circular base.
Gauss's Law states that the total electric flux Φ through a closed surface is equal to the charge enclosed Qin divided by the permittivity of free space ϵ0:
Φ=Qinϵ0
Since the hemisphere is not a closed surface, we can imagine completing the hemisphere into a full sphere by adding an identical hemisphere. Thus, we can treat the entire sphere as a closed surface.
For the entire sphere, the charge Q is enclosed, so the total electric flux through the sphere is:
Φsphere=Qϵ0
Since the flux is uniformly distributed over the entire surface of the sphere, the flux through the hemisphere (which is half of the sphere) is:
Φhemisphere=12Φsphere=12(Qϵ0)=Q2ϵ0
The total flux through the hemisphere includes both the curved surface and the flat surface. However, due to symmetry, the flux through the flat surface is equal to the flux through the curved surface.
Φflat=12Φhemisphere=12(Q2ϵ0)=Q4ϵ0
The electric flux passing through the flat surface of the hemisphere is:
Φflat=Q4ϵ0
Topper's Solved these Questions
- BOOK - BITSAT GUIDECHAPTER - GAUSS LAW AND ELECTRIC POTENTIAL THEORYEXERCISE - BITSTAT ARCHIVES4videos
GAUSS LAW AND ELECTRIC POTENTIAL THEORY
- BOOK - BITSAT GUIDECHAPTER - FLUID MECHANICSEXERCISE - BITSAT Achives15videos
FLUID MECHANICS
- BOOK - BITSAT GUIDECHAPTER - MAGNETIC FIELDEXERCISE - All Questions52videos
MAGNETIC FIELD
Similar Questions
Knowledge Check
- Question 1 - Select One
An electric dipole is placed at the centre of a sphere. Find the electric flux passing through the sphere.
A0B1C2DNone of the above - Question 2 - Select One
Charge of 2 C is placed at the centre of a cube. What is the electric flux passing through one face ?
A1(3ε0)B(14)ε0C2ε0D3ε0 - Question 3 - Select One
In figure (a), a charge q is placed just outside the centre of a closed hemisphere. In figure (b), the same charge q is placed just inside the centre of the closed hemisphere and in figure (c), the charge is placed at the centre of hemisphere open from the base. Find the electric flux passing through the hemisphere in all the three cases.
 A0 , qε0 q2ε0B0 , 0 q2ε0C0 , qε0 0D0 , 0 0
A0 , qε0 q2ε0B0 , 0 q2ε0C0 , qε0 0D0 , 0 0
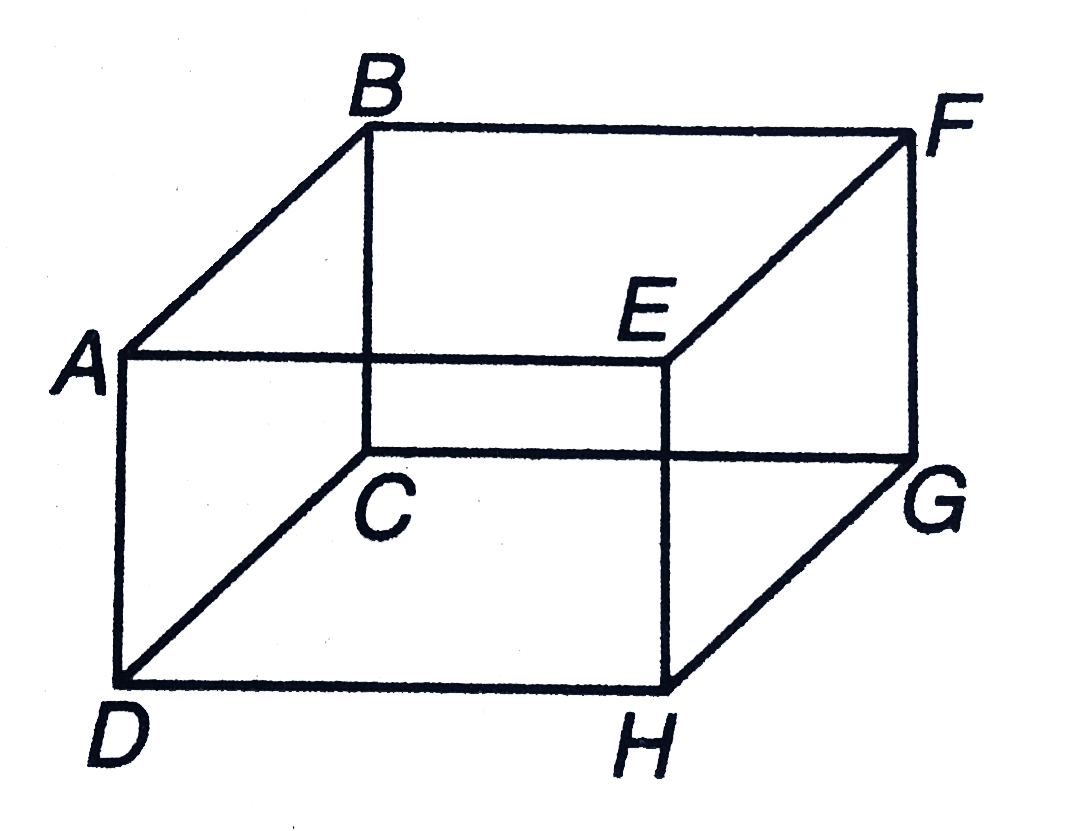
A charge q is placed at point D of the cube. Find the electric flux passing through the EFGH and face AEHD.
 View Solution
View SolutionA charge q is placed at the centre of a cube of side l what is the electric flux passing through two opposite faces of the cube ?
View SolutionA chrage 'q' is placed at the centre of a cube of side 'l' . What is the electric flux passing through each face of the cube?
View SolutionIf electric flux passing through a close surface is zero then :-
View SolutionA charge q is placed at the centre of a hollow sphere of radius r, Total electric flux passing through the spherical surface is __________
View Solution

