An infinite plane sheet of positive charge has surface charge density σ. A metallic ball of mass m and charge +Q is attached to a thred and is tied to a point A on the sheet PQ. The angle θ made by the string with plane sheet is in equilibrium is
zero
tan−1(Qσ4ε0mg)
tan−1(Qσ2ε0mg)
tan−1(Qσε0mg)
To solve the problem, we need to analyze the forces acting on the metallic ball attached to the thread and determine the angle θ that it makes with the plane sheet when in equilibrium.
1. Identify the Forces Acting on the Ball:
- The ball experiences two main forces:
- The gravitational force (weight) acting downwards: Fg=mg
- The electric force due to the infinite plane sheet: Fe=Q⋅E
2. Determine the Electric Field (E) Due to the Plane Sheet:
- The electric field due to an infinite plane sheet with surface charge density σ is given by:
E=σ2ϵ0
- Therefore, the electric force acting on the ball is:
Fe=Q⋅E=Q⋅σ2ϵ0
3. Set Up the Force Balance:
- Since the ball is in equilibrium, the net force in the vertical direction must equal the net force in the horizontal direction. The tension in the thread can be resolved into two components:
- Vertical component: Tcos(θ)=mg
- Horizontal component: Tsin(θ)=Fe
4. Relate the Forces:
- From the vertical component:
Tcos(θ)=mg(1)
- From the horizontal component:
Tsin(θ)=Q⋅σ2ϵ0(2)
5. Divide Equation (2) by Equation (1):
- To eliminate T, we divide the two equations:
Tsin(θ)Tcos(θ)=Q⋅σ2ϵ0mg
- This simplifies to:
tan(θ)=Q⋅σ2ϵ0mg
6. Solve for θ:
- Taking the inverse tangent gives us:
θ=tan−1(Qσ2ϵ0mg)
Final Result:
The angle θ made by the string with the plane sheet in equilibrium is:
θ=tan−1(Qσ2ϵ0mg)
- The ball experiences two main forces:
- The gravitational force (weight) acting downwards: Fg=mg
- The electric force due to the infinite plane sheet: Fe=Q⋅E
- The electric field due to an infinite plane sheet with surface charge density σ is given by:
E=σ2ϵ0
- Therefore, the electric force acting on the ball is:
Fe=Q⋅E=Q⋅σ2ϵ0
- Since the ball is in equilibrium, the net force in the vertical direction must equal the net force in the horizontal direction. The tension in the thread can be resolved into two components:
- Vertical component: Tcos(θ)=mg
- Horizontal component: Tsin(θ)=Fe
- From the vertical component:
Tcos(θ)=mg(1)
- From the horizontal component:
Tsin(θ)=Q⋅σ2ϵ0(2)
- To eliminate T, we divide the two equations:
Tsin(θ)Tcos(θ)=Q⋅σ2ϵ0mg
- This simplifies to:
tan(θ)=Q⋅σ2ϵ0mg
- Taking the inverse tangent gives us:
θ=tan−1(Qσ2ϵ0mg)
The angle θ made by the string with the plane sheet in equilibrium is:
θ=tan−1(Qσ2ϵ0mg)
Topper's Solved these Questions
Similar Questions
Field Of An Infinite Plane Sheet Of Charge
View SolutionThe line AA' is on a charged infinite conducting plane which is perpendicular to the plane of the paper. The plane has surface density of charge σ and B is a ball of mass m with a like charge of magnitude q. B is connected by a string from a point on the line AA'. The tangent of the angle (θ) formed between the line AA' and the string is (provided, the charge q does not affect the distribution of charge on conducting plate)
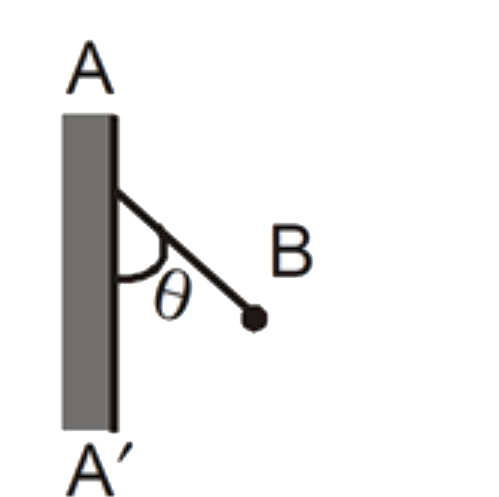 View Solution
View Solution
Knowledge Check
- Question 1 - Select One or More
Two infinite plane sheets of charge A and B of positive charge have surface charge densities Kσandσ, respectively. A metallic ball of mass m and charge +q is attached to a thread and the thread is tied at point P on sheet A. Initially ball is equilibrium at plate P when sheets are uncharged. Find the correct options (K is a constant.)
 AIf K>1,∠θ=tan−1(Kσg)2ε0mg.BIf Klt1, the ball will not leave its equilibrium.CIf K = 1, the angle θ=45∘.DIf Kgt1, the angle θ=tan−1((K−1)σg)2ε0mg
AIf K>1,∠θ=tan−1(Kσg)2ε0mg.BIf Klt1, the ball will not leave its equilibrium.CIf K = 1, the angle θ=45∘.DIf Kgt1, the angle θ=tan−1((K−1)σg)2ε0mg - Question 2 - Select One
An infinite sheet of charge has surface charge density σ . The separation between two equipotential surfaces, whose potential differ by V is:
AσV2∈0B2∈0VσC∈0VσD2σ∈0V - Question 3 - Select One
Two uniform sheets of charge with surface charge densities +σ and −σ are intersecting at right angles to each other. Electric field intensity due to this system is
Aσ2ε0Bσ2√2ε0Cσε0√2DNone
a)State Gauss’s law in electrostatics. Show that with help of suitable figure that outward flux due to a point charge Q, in vacuum within gaussian surface, is independent of its size and shape.
b) In the figure there are three infinite long thin sheets having surface charge density +2σ,−2σand+σ respectively. Give the magnitude and direction of electric field at a point to the left of sheet of charge density +2σ and to the right of sheet of charge density +σ
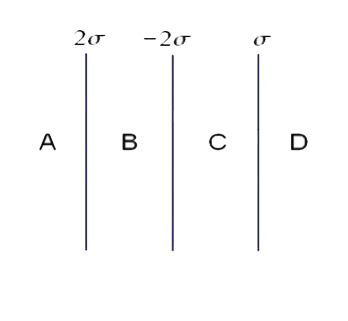 View Solution
View SolutionA large flat metal surface has a uniform charge density (+σ). An electron of mass m and charge ρ leaves the surface at the point A with speed u and returns to it at point B. Disregarding gravity the maximum value of AB is
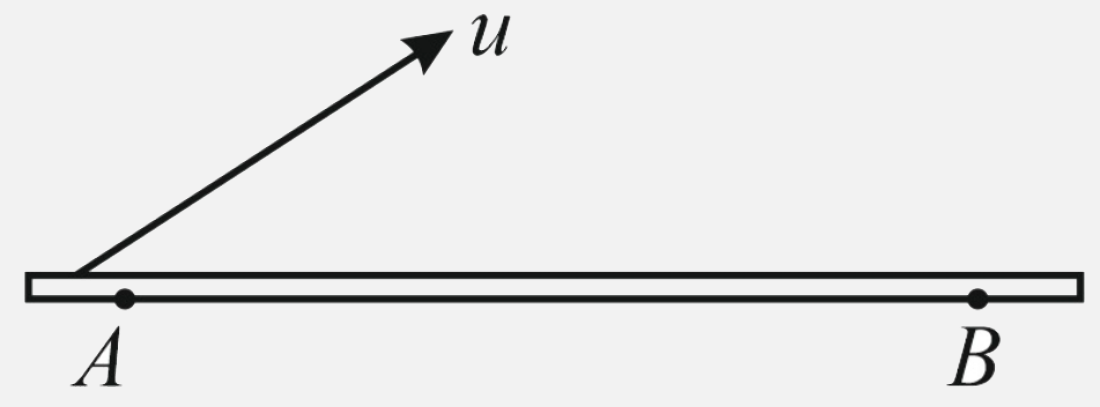 View Solution
View SolutionIn the figure shown there is a large sheet of charge of uniform surface charge density'σ'.A charge particle of charge '−q' and mass 'm' is projected from a point A on the sheet with a speed 'u' with the angle of projection such that it lands at maximum distance from A on the sheet. Neglecting gravity, find the time flight
 View Solution
View SolutionConsider an infinite plane sheet of mass with surface mass density σ. The gravitational field intensity at a point P at perpendicular distance r from such a sheet is :
View SolutionAn injfinite large sheet has charg density σC/m2 Find electric field at a distance d perendicular to the sheet.
View Solution

