Given, β=49 and le= 2ma, lc for a BJT is
2 mA
1.96 mA
98 mA
249 mA
The correct Answer is:B
β=49,le=2mA,lc=?
β=(lclb),α=(lcle)
α=(β1+β=491+49=4950
4950=(lcle)
lc=49×250 mA
lc=1.96mA
Topper's Solved these Questions
- BOOK - BITSAT GUIDECHAPTER - SEMICONDUCTOR DEVICES AND LOGIC GATESEXERCISE - BITSAT Archives5videos
SEMICONDUCTOR DEVICES AND LOGIC GATES
- BOOK - BITSAT GUIDECHAPTER - RAY OPTICSEXERCISE - All Questions39videos
RAY OPTICS
- BOOK - BITSAT GUIDECHAPTER - SOLVED PAPER 2017 EXERCISE - (PART -I) PHYSICS40videos
SOLVED PAPER 2017
Similar Questions
Two bodies with moment of inertia l1 and l2 (l1>l2) have equal angular momentum. If E1 and E2 are the rotational kinetic energies, then
View SolutionIn the following network of 5 branches, the respective current are l1,l2,l3 etc. given that l1=−0.5A,l4=1A and l5=0.5A, the remaining currents are
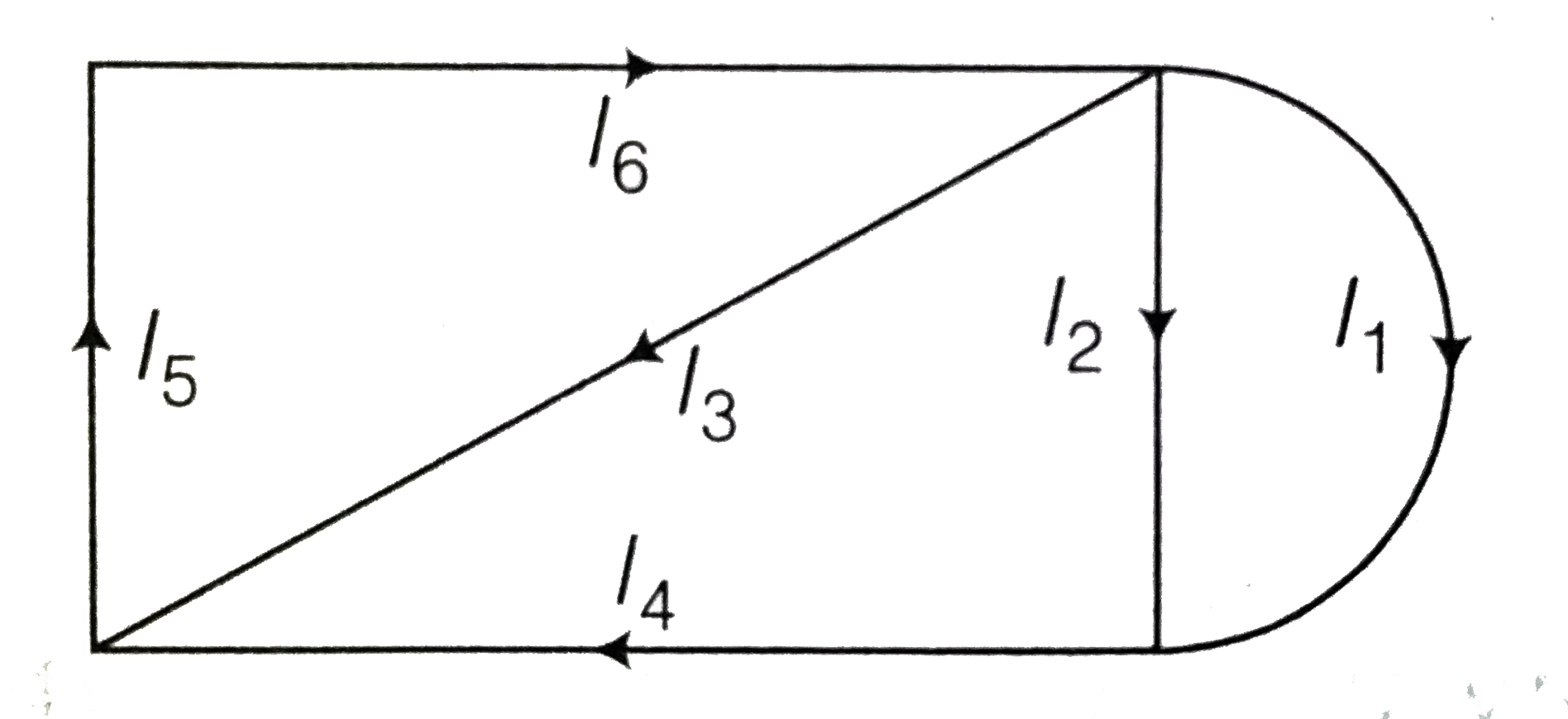 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two alternating current are given by
l1=l0 sin ωtand l l_(2)=l_(0) cos (omega +phi)
The ratio of rms value isA0.042361111111111B1:ϕC0.043055555555556Dnon of these - Question 2 - Select One
Given : li=44.2±=0.1 and l2=23.1±0.1 the uncertainty in l1+l2 is
A0B0.1C0.2D0.4 - Question 3 - Select One
If the frequency of Kα,Kβ and Lα , X-ray lines of a substance are vKα,vKβ, and vLβ
AvKα+vKβ=vLαBvKα−vKβ=vLαCvKα+vLα=vKβDnone of these
Let C:x2−3,D:y=kx2 be two parabolas and
L1 : xa,L2:x=1(a≠0) be two straight lines.
IF the line L1 meets the parabola C at a point B on the line L2, other than A, then a may be equal toView SolutionLet L be the set of all straight lines in plane. l1 and l2 are two lines in the set. R1,R2 and R3 are defined relations.
(i) l1R1l2:l1 is parallel to l2
(ii) l1R2l2:l1 is perpendicular to l2
(iii) l1R3l2:l1 intersects l2
Then which of the following is true ?View SolutionFor a vacuum triode, the values of Ec, Eb and lb are given as under

The values of μ and rp are given byView SolutionIf λKα,λKβ and λLα are the wavelengths of Kα,Kβ and Lα, lines respectively , then
View SolutionConsider the lines
L1:x+y=10, L2:x+y=60
L3:x=40, L4:y=40.
L1 meets x - axis and y - axis at A and B respectively.
L4 meets y - axis at C and L2 at D
L3 meets L2 at E and x-axis at F.
Perimeter of the hexagon ABCDEF isView Solution

