A cannon of mass 1000 kg located at the base of an inclined of an inclined plane fires a shell of mass 100 kg in a horizontal direction with a velocity 180 km//hr.The angle of inclination of inclined plane with the horizontal is $45^{\circ}$ . The coefficient of friction between the canon and inclined plane is 0.5. The height in meter to which the cannon ascends the inclined plane as a result of recoil is $(g = 10 m / s^{2}$ )

Text Solution

Verified by Experts

The correct Answer is: $6.00$

Momentum of cannon after recoil $\times$ Momentum of shell
$= 100 \times 180 \times \frac{5}{18}$
$= 5000$ kg-m/s
Velocity of recoil of cannon $= \frac{5000}{1000} = 5 m / s$
Let the cannon ascends a distance s on the rough inclined surface.The effective deceleration is

$a = \frac{μ R + M g {\sin 45}^{\circ}}{M}$
$a = \frac{m j M g {\cos 45}^{\circ} + M g {\sin 45}^{\circ}}{M}$
$a = \frac{g}{\sqrt{2}} [μ + 1]$
$v^{2 () = u^{2} = 2 a s}$
$0 = {(5)}^{2} - 2 \times \frac{g}{\sqrt{2}} (μ + 1) s$
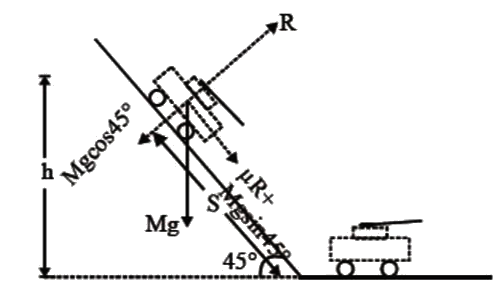
or $s = \frac{25}{\sqrt{2} \times 10 (0.5 + 1)} = \frac{25}{\sqrt{2} \times 15} = \frac{5}{3 \sqrt{2}} m$
Now $h = s . {\sin 45}^{\circ} = \frac{5}{3 \sqrt{2}} \times \frac{1}{\sqrt{2}} = \frac{5}{6} m$

|

Updated on:21/07/2023

Class 12 PHYSICS DRILL-TEST

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A cannon of mass $1000 k g$ located at the base of an inclined plane fires a shell of mass $50 k g$ in horizontal direction with velocity $180 k m / h$ . The angle of inclination of the inclined plane with the horizontal is $45^{\circ}$ . The coefficient of friction between the cannon and inclined plane is $0.5$ . The maximum height, in metre, to which the cannon can ascend the inclined plane as a result of recoil is
A $\frac{5}{6}$
B $\frac{5}{24}$
C $\frac{5}{12}$
Dnone of these
Question 2 - Select One
A cannon of mass 2m located at the base of an inclined plane shoots a shell of mass m in horizontal direction with velocity $v_{0}$ The angle of inclination of plane is $45^{\circ}$ and the coefficient of friction between the cannon and the plane is $0.5$ The height to which cannon ascends the plane as a result of recoil is :
A $\frac{v_{0}^{2}}{2 g}$
B $\frac{v_{0}^{2}}{12 g}$
C $\frac{v_{0}^{2}}{6 g}$
D $\frac{v_{0}^{2}}{g}$
Question 3 - Select One
A block of mass $m$ is placed at rest on an inclination $θ$ to the horizontal.If the coefficient of friction between the block and the plane is $μ$ , then the total force the inclined plane exerts on the block is
A $m g$
B $μ m g cos θ$
C $m g sin θ$
D $μ m g tan θ$

NEET MAJOR TEST (COACHING)-DRILL-TEST-PHYSICS

Home
Ask Doubt
Profile