A particle is moving in a vertical in a vertical circle . The tensions in the string when passing through two positions at angles $30^{\circ} and 60^{\circ}$ from the lowest positon are $T_{1} and T_{2}$ respectively , then

A

$T_{1} = T_{2}$

B

$T_{1} > T_{2}$

C

$T_{1} < T_{2}$

D

$T_{1} \geq T_{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

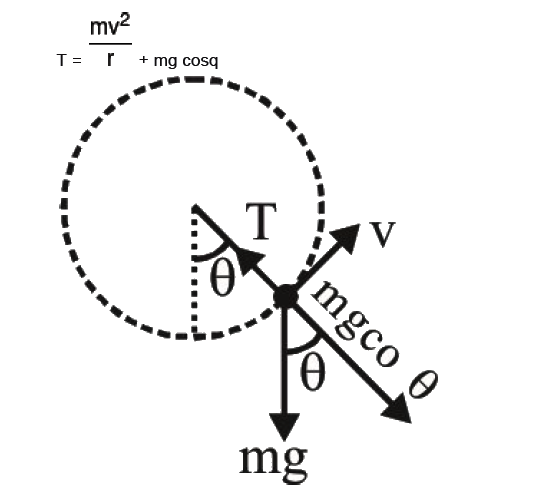
$T = \frac{m v^{2}}{r} + m g cos q$
as $θ$ increases $cos θ and v$
both decreases
hence for $θ = 60^{\circ}$ , T will be less, i.e., $T_{1} \geq T_{2}$ .

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle is moving in a vertical circle with constant speed. The tansions in the string when passing through two positions at angles $30^{\circ}$ and $60^{\circ}$ from vertical (lowest position) are $T_{1}$ and $T_{2}$ respectively. Then
A $T_{1} = T_{2}$
B $T_{2} > T_{1}$
C $T_{1} > T_{2}$
DTension in the string always remains the same
Question 2 - Select One
If a bodyy is tied to a string and whirled in vertical circle, then the tension in the string at the highest position is
Amaximum
Bminimum
Cbetween maximum and minimum values
Dzero
Question 3 - Select One
A particle of mass m is rotating by means of a string in a vertical circle . The difference in tension at the top and the bottom revolution is
A6 mg
B4 mg
C2 mg
D3 mg

NEET MAJOR TEST (COACHING)-NEET-UG DRILL TEST 14-PHYSICS

Home
Ask Doubt
Profile