Consider f:(0,∞)→(−π2,π2), defined as f(x)=tan−1(logex(logex)2+1). The about function can be classified as
Video Solution
|
Answer
Step by step video & image solution for Consider f:(0, oo)->(-pi/2,pi/2), defined as f(x) = tan^-1 (log_e x/((log_e x)^2+1)). The about function can be classified as by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
f:(0,∞)→(−π2,π2) be defined as, f(x)=tan−1(logex).
The above function can be classified as :Ainjective but not surjectiveBsurjective but not injectiveCneither injective nor surjectiveDboth injective as well as surjectivef:(0,∞)→(−π2,π2) be defined as, f(x)=tan−1(logex).
The graph of y = f (x) is best represented byA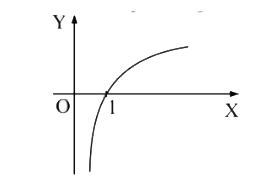 B
B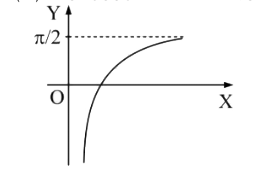 C
C D
D
f:(0,∞)→(−π2,π2) be defined as, f(x)=tan−1(logex).
If x1,x2andx3 are the points at which g(x) =[f (x)] is discontinuous (where, [.] denotes the greatest integer function), then (x1+x2+x3) is :A2B3Cgreater than 3Dbelong to
f:(0,∞)→(−π2,π2) be defined as, f(x)=tan−1(logex).
The graph of y = f (x) is best represented by
View Solutionf:(−π2,π2)→(−∞,∞) defined by f(x)=tanx is
View Solutionf:(0,∞)→(−π2,π2) be defined as, f(x)=tan−1(logex).
If x1,x2andx3 are the points at which g(x) =[f (x)] is discontinuous (where, [.] denotes the greatest integer function), then (x1+x2+x3) is :
View SolutionIf f(x)=cos−1{1−(logex)21+(logex)2}, then f'( e )
View SolutionIf f(x)=cos−1{1−(logex)21+(logex)2}, then f'( e )
View Solution
