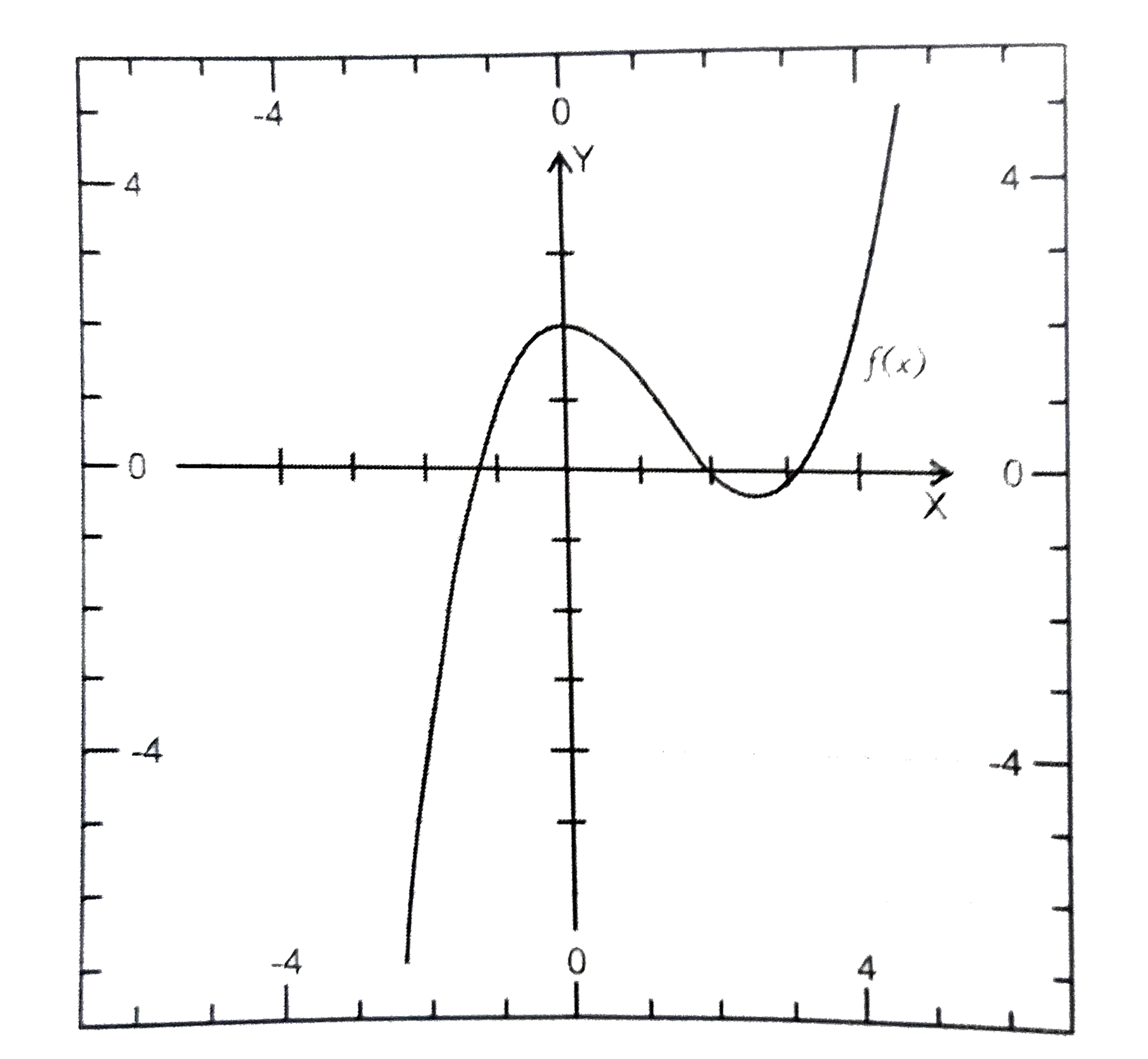
What is the number of possible values of K (5>k>0) such that g(x) = f(x) -k has exactly one root ?
The correct Answer is:2
Topper's Solved these Questions
Similar Questions
The sum of all possible integral value of 'k' for which 5x2−2kx+1<0 has exactly one integral solution :
View SolutionLet f(x) is a real valued function defined on R such that f(x)=√4+√16x2−8x3+x4 . The number of integral values of 'k' for which f(x)=k has exactly 2 distinct solutions for k in [0,5] is
View Solution
Knowledge Check
The possible positive integral value of 'k' for which 5x2−2kx+1<0 has exactly one integral solution may be divisible by :
A2B3C5D7
Find the values of k so that the quadratic equation x2+2(k−1)x+k+5=0has atleast one positive root
View SolutionFind the value of k so that the equation 2x2−5x+k=0 has two equal roots.
View SolutionFind the values of k for which the equation x2+5kx+16=0 has no real roots.
View SolutionFind the value of k such that x2+2x+9k−5=0 has both roots negative.
View SolutionLet f(x)=x2−9−|x−a| . If the number of integers in the range of a so that f(x)=0 has 4 distinct real root is K ,then [K5]=, ([.] denotes G.I.F)
View SolutionIf k1 and k2 (k1>k2) are two non-zero integral values of k for which the cubic equation x3+3x2+k=0 has all integer roots, then the value of k1−k2 is equal to_______
View SolutionIf k1 and k2 (k1>k2) are two non-zero integral values of k for which the cubic equation x3+3x2+k=0 has all integer roots, then the value of k1−k2 is equal to_______
View Solution
