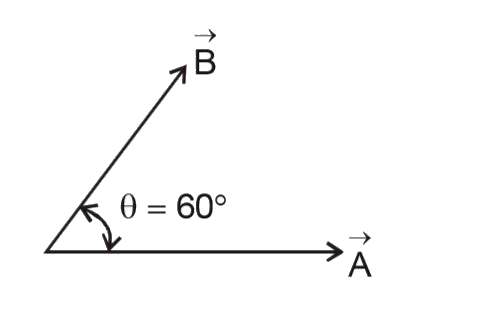
Find →A+→Band→A−→B in the diagram shown in figure. Given A = 4 units and B = 3 units.
Video Solution
Text Solution
Addition : R=√A2+B2+2ABcosθ
√16+9+2×4×3cos60∘=√37 units
tanα=BsinθA+Bcosθ=3sin60∘4+3cos60∘=0.472
∴α=tan−1(0.472)=25.3∘
Thus, resultant of →Aand→B is √37 units at angle 25.3∘ from →A in the direction shown in figure.
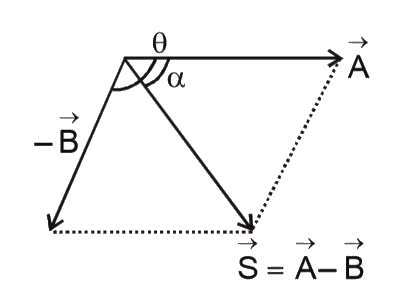
Subtraction:
S=√A2+B2−2ABcosθ
√16+9−2×4×3cos60∘
=√13 units
and
tanθ=BsinθA−Bcosθ
=3sin60∘4−3cos60∘=1.04
∴α=tan−1(1.04)=46.1∘
Thus, resultant of →Aand→B is √13 units at 46.1∘ from →A in the direction shown in figure.
|
Topper's Solved these Questions
- VECTOR & CALCULUSBOOK - MOTIONCHAPTER - VECTOR & CALCULUSEXERCISE - PHYSICAL EXAMPLE
11 Videos
- VECTOR & CALCULUSBOOK - MOTIONCHAPTER - VECTOR & CALCULUSEXERCISE - EXERCISE -1
76 Videos
- VECTOR BOOK - MOTIONCHAPTER - VECTOR EXERCISE - Exercise - 3
18 Videos
- WAVE MOTION BOOK - MOTIONCHAPTER - WAVE MOTION EXERCISE - Exercise - 3 Section - B (Previous Years Problems)
7 Videos
Similar Questions
Knowledge Check
If ∣∣→A∣∣=4,∣∣→B∣∣=3andθ=60∘ in the figure . Find
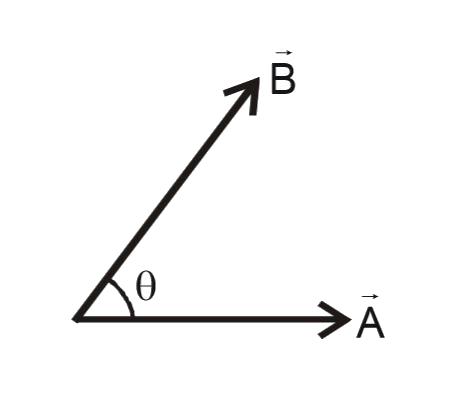
→A.→BA6B3C9D12If →A=→B+→C and the magnitudes of →A,→Band→C are 5,4 and 3 units respecetively, the angle between →A and →C is :
Acos−1(3/5)Bcos−1(4/5)Cπ/2Dsin−1(3/4)If →a,→b are unit vectors such that the vector →a+3→b is peependicular to 7→a−→band→a−4→b is prependicular to 7→a−2→b then the angle between →aand→b is
Aπ/6Bπ/4Cπ/3Dπ/2
Let →a and →b be two vectors such that ∣∣2→a+3→b∣∣=∣∣3→a+→b∣∣ and the angle between →a and →b is 60∘ . If 18→a is a unit vector, then ∣∣→b∣∣ is equal to :
View SolutionGiven →a,→band→c are 3 vectors such that →b,→c are parallel unit vectors and |→a|=3. If →a+λ→c=4→b, then the sum of all the possible positive values of λ is
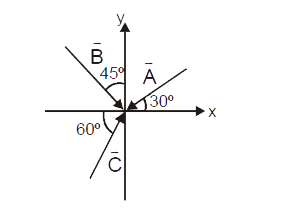
View SolutionThree vectors →A,→B,→C are shown in the figure. Find angle between
(i) →A and →B (ii) →B and →C (iii) →A and →C.
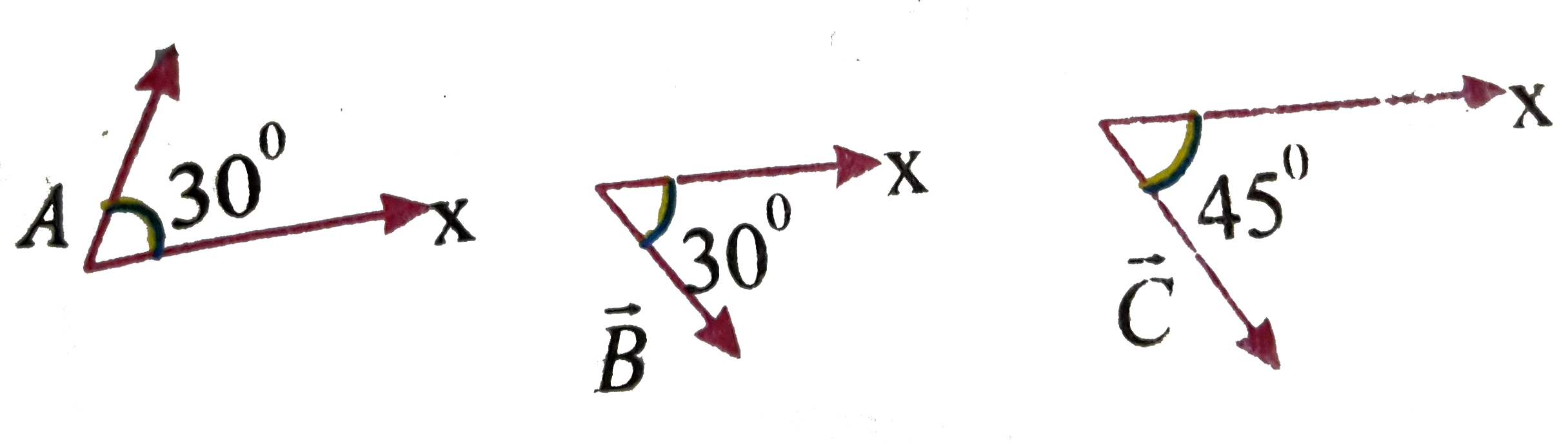
View SolutionIf →aand→b are any two unit vectors, then find the greatest postive integer in the range of 3∣∣→a+→b∣∣2+2∣∣→a−→b∣∣
View SolutionGiven : →C=→A+→B . Also , the magnitude of →A,→Band→C are 12,5 and 13 units respectively . The angle between →Aand→B is
View Solution