If →Aand →B have angle between them equals to 60∘ and their resultant make, angle 45∘ with →Aand→A have magnitude equal to 10. Then Find magnitude of →B.
Video Solution
Text Solution
Here α=45∘andβ=60∘−45∘=15∘
so Asinα=Bsinβ
10sin45∘=Bsin45∘
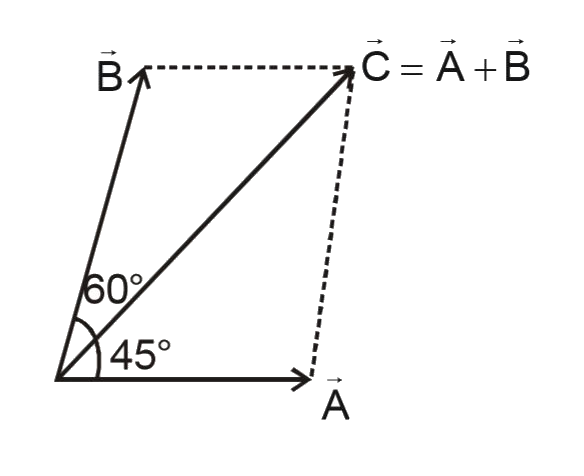
SoB=10√2sin15∘
=10√2√1−cos(2×15)2=5√2√2−√3.
|
Topper's Solved these Questions
- VECTOR & CALCULUSBOOK - MOTIONCHAPTER - VECTOR & CALCULUSEXERCISE - PHYSICAL EXAMPLE
11 Videos
- VECTOR & CALCULUSBOOK - MOTIONCHAPTER - VECTOR & CALCULUSEXERCISE - EXERCISE -1
76 Videos
- VECTOR BOOK - MOTIONCHAPTER - VECTOR EXERCISE - Exercise - 3
18 Videos
- WAVE MOTION BOOK - MOTIONCHAPTER - WAVE MOTION EXERCISE - Exercise - 3 Section - B (Previous Years Problems)
7 Videos
Similar Questions
Knowledge Check
What is the angle between →a and the resultant of →a+→b and →a−→b ?
A0Btan−1abCtan−1baDtan−1(a−b)(a+b)The resultant of →Aand→B makes an angle alpha with →A and βand→B,
Aα<βBα<βifA<BCα<βifA<βDα<betifA=B.If the resultant of →A and →B makes angle α with →A and β with →B, then
Aα<β alwaysBα<β if A<BCα<β if A>BDα<β if A=B
The resultant of →A and →B makes an angle α with →Aand→β with →B, then -
View SolutionIf the angle between the vectors →Aand→B is θ, the value of the product (→B×→A)⋅→A is equal to
View SolutionIf the angle between the vectors →Aand→B is θ, the value of the product (→B×→A)⋅→A is equal to
View SolutionTwo vectors →Aand→B inclined at an angle θ have a resultant →R which makes an angle α with →A and angle β with →B. Let the magnitudes of the vectors →A,→Band→R be represented by A, B and R respectively. Which of the following relations is not correct ?
View SolutionIf ∣∣→A+→B∣∣=∣∣→A∣∣+∣∣→B∣∣, then angle between →A and →B will be
View Solution
