Evaluate $\int \sqrt{x^{2} + 2 x + 5} d x$

Video Solution

Text Solution

Verified by Experts

If we recognize that $(x^{3} / 3) - x^{2} + 5 x$ is an antiderivative of $x^{2} - 2 x + 5$ , we can evaluate the integral as

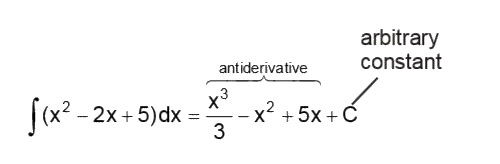
If we do not recognize the antiderivative right away, we can generate it term by term with the sum and difference Rule :
$\int (x^{2} - 2 x + 5) d x = \int x^{2} d x = \int x^{2} d x - \int 2 x d x + \int 5 d x$
$= \frac{x^{3}}{3} + C_{1} - x^{2} + C_{2} + 5 x + C_{3}$
This formula is more complicated than it needs to be. If we combine $C_{1}, C_{2} and C_{3}$ into a single constant $C = C_{1} + C_{2} + C_{3}$ , the formula simplifies to
$\frac{x^{3}}{3} - x^{2} + 5 x + C$
and still gives all the antiderivatives there are. For this reason we recommend that you go right to the final form even if you elect to integrate term by term. Write
$\int (x^{2} - 2 x + 5) d x = \int x^{2} d x - \int 2 x d x + \int 5 d x$
$= \frac{x^{3}}{3} - x^{2} + 5 x + C$ .
Find the simplest antiderivative you can for each part add the constant at the end.

|

Updated on:21/07/2023

Class 12 PHYSICS VECTOR & CALCULUS

Topper's Solved these Questions

Similar Questions

MOTION-VECTOR & CALCULUS-PHYSICAL EXAMPLE

Home
Ask Doubt
Profile