Question

Using an area to evaluate a definite integral.
Evaluate ${\int }_z^{b}xdx0<a<b$.

Explanation

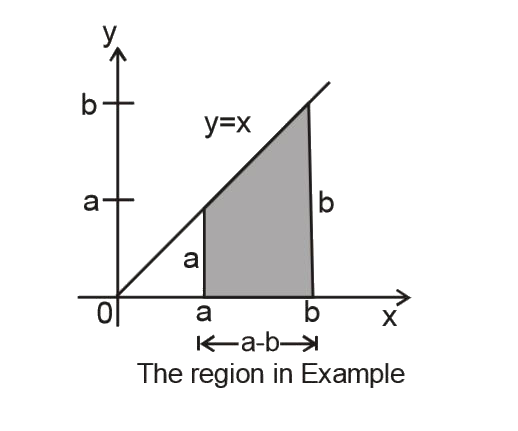
We sketch the region under the curve `y = x, a le x le b` (figure) and see that it is a trapezoid with height (b – a) and bases a and b. The value of the integral is the area of this trapezoid :
Thus `int_(a)^(b) xdx = (b - a) (a +b)/2 = (b^2)/2 - (a^2)/2`

`int_(1)^(sqrt(5)) xdx = ((sqrt(5)^2)/(2) - ((1)^(2))/(2) = 2`
and so on.
Notice that `x^2//2` is an antiderivative of x, further evidence of a connection between antiderivatives and summation.