Vector $\to R$ is the resultant of the vetors $\to A and \to B$ . Ratio of maximum value of $∣ ∣ \to R ∣ ∣$ to the minimum value of $∣ ∣ \to R ∣ ∣$ is $\frac{3}{1}$ . The $\frac{∣ ∣ \to A ∣ ∣}{∣ ∣ \to B ∣ ∣}$ may be equal to-

A

$\frac{2}{1}$

B

$\frac{1}{2}$

C

$\frac{4}{1}$

D

$\frac{3}{1}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B

|

Answer

Step by step video, text & image solution for Vector vecR is the resultant of the vetors vecA and vecB. Ratio of maximum value of |vecR| to the minimum value of |vecR| is 3/1. The (|vecA|)/(|vecB|) may be equal to- by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS VECTOR & CALCULUS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
$\to R$ is the resultant of $\to A$ and $\to B$ . $\to R$ is inclined to $\to A$ at angle $t h e a t_{1}$ and to $\to B$ at angle $θ_{2}$ , then :
A $θ_{1} < θ_{2}$
B $θ_{1} < θ_{2} if A > B$
C $θ_{1} < θ_{2} if A < B$
D $θ_{1} < θ_{2} if A = B$
Question 2 - Select One
In vector diagram shown in figure where $(\to R)$ is the resultant of vectors $(\to A)$ and $(\to B)$ . If $R = \frac{B}{\sqrt{2}}$ , the value of angle $θ$ is :

A $30^{\circ}$
B $45^{\circ}$
C $60^{\circ}$
D $75^{\circ}$
Question 3 - Select One
In vector diagram shown in figure where $(\to R)$ is the resultant of vectors $(\to A) and (\to B)$ .

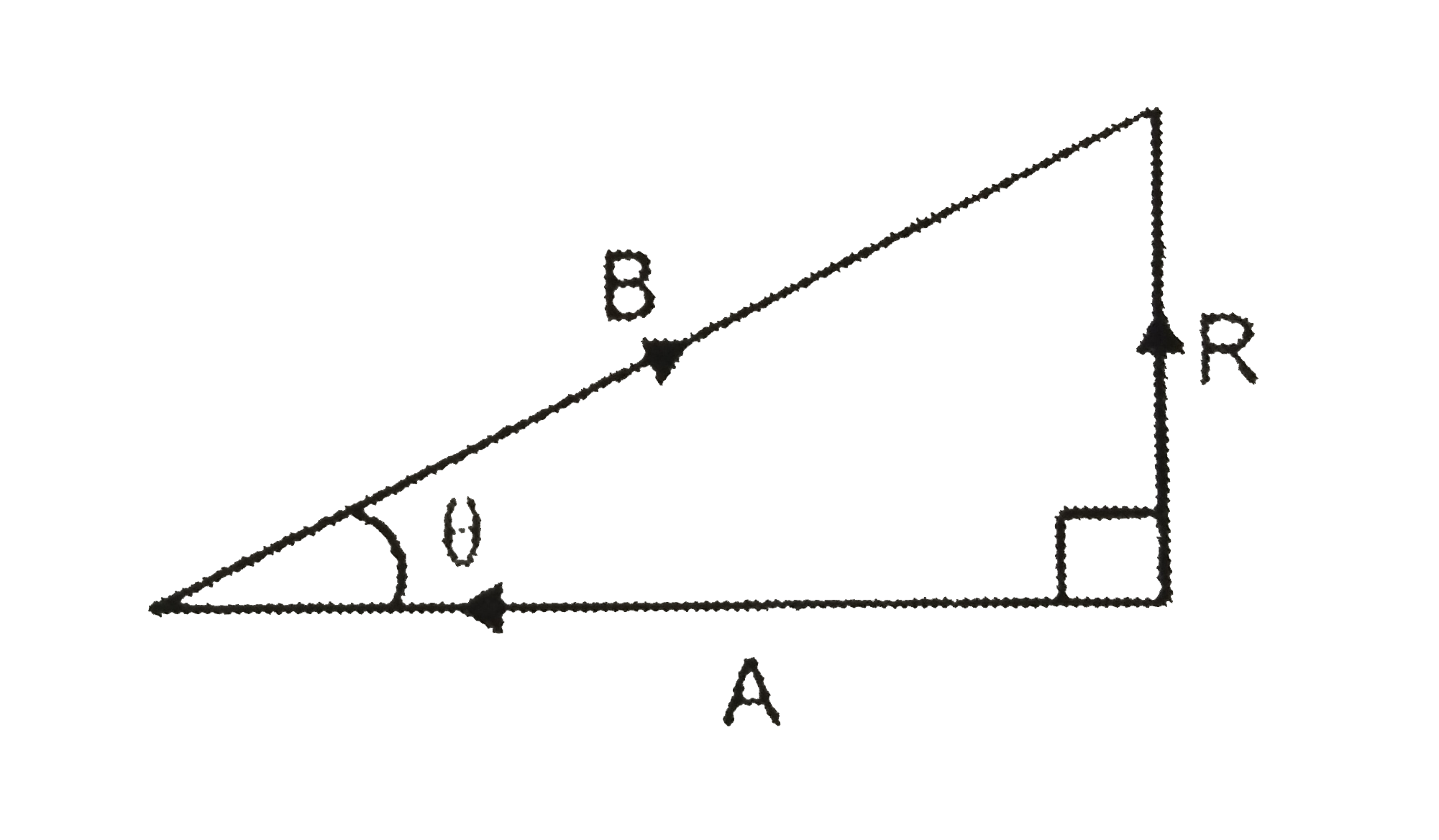
If $R = \frac{B}{\sqrt{2}}$ , then value of angle $θ$ is :
A $30^{\circ}$
B $45^{\circ}$
C $60^{\circ}$
D $75^{\circ}$

MOTION-VECTOR & CALCULUS-EXERCISE -2 (LEVEL - II) MULTIPLE CORRECT

Home
Ask Doubt
Profile