Question

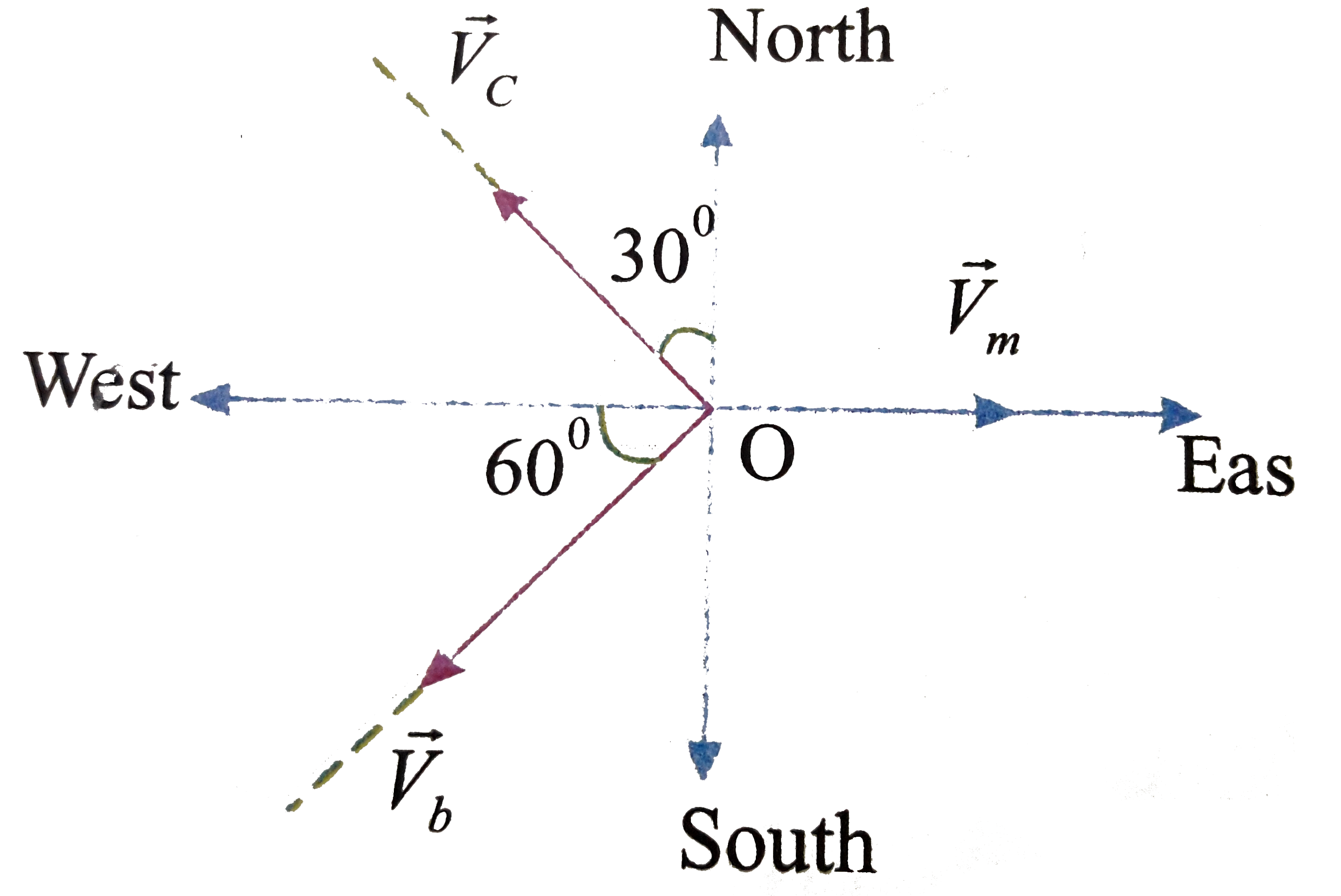
A man is walking toward east with a velocity of 8 km/h. Wind is blowing toward north - east at angle of ${45}^{\circ }$. To the man wind appears to blow of angle of ${60}^{\circ }$ north of west.

Options

A. True velocity of wind is `(8sqrt(6))/(1+sqrt(3))` km/hr
B. Velocity of wind relative to man is `(16)/(1+sqrt(3))` km/h
C. True velocity of wind is `(sqrt(6))/(1+sqrt(3))` km/h
D. Velocity of wind relative to man is `(8sqrt(3))/(1+sqrt(3))` km/h

Answer

A::B

Explanation

To solve the problem step by step, we need to analyze the situation involving the man walking and the wind blowing.

Step 1: Define the Velocities
- Let the velocity of the man \( V_m \) be \( 8 \, \text{km/h} \) towards the east.
- Let the velocity of the wind \( V_w \) be at an angle of \( 45^\circ \) towards the north-east.

Step 2: Resolve the Wind Velocity
The wind's velocity can be resolved into its components:
- The wind's velocity components can be expressed as:
\( V_{wx} = V_w \cos(45^\circ) = \frac{V_w}{\sqrt{2}} \quad \text{(east component)} \)
\( V_{wy} = V_w \sin(45^\circ) = \frac{V_w}{\sqrt{2}} \quad \text{(north component)} \)

Step 3: Relative Velocity of Wind
To the man, the wind appears to blow at an angle of \( 60^\circ \) north of west. We need to express this relative velocity \( V_{wr} \):
- The relative velocity components can be expressed as:
\( V_{wr} = V_{wx} - V_m \quad \text{(east component)} \)
\( V_{wy} = V_{wr} \tan(60^\circ) \quad \text{(north component)} \)

Step 4: Set Up Equations
From the above, we can set up the equations based on the components:
1. For the east component:
\( V_{wr} = \frac{V_w}{\sqrt{2}} - 8 \)
2. For the north component:
\( V_{wy} = V_{wr} \sqrt{3} \quad \text{(since } \tan(60^\circ) = \sqrt{3}\text{)} \)

Step 5: Substitute and Solve
Substituting \( V_{wr} \) from the first equation into the second:
\( \frac{V_w}{\sqrt{2}} \tan(60^\circ) = \frac{V_w}{\sqrt{2}} - 8 \)
This leads to:
\( V_w \sqrt{3} = \frac{V_w}{\sqrt{2}} - 8 \)

Step 6: Rearranging the Equation
Rearranging gives:
\( V_w \left( \frac{1}{\sqrt{2}} - \sqrt{3} \right) = 8 \)
Thus,
\( V_w = \frac{8}{\frac{1}{\sqrt{2}} - \sqrt{3}} \)

Step 7: Rationalizing the Denominator
To simplify, multiply the numerator and denominator by \( \sqrt{2} \):
\( V_w = \frac{8\sqrt{2}}{1 - \sqrt{6}} \)

Step 8: Final Result
The true velocity of the wind is:
\( V_w = 8\sqrt{2} \cdot \frac{1 + \sqrt{6}}{-5} = \frac{8\sqrt{2}(1 + \sqrt{6})}{5} \)