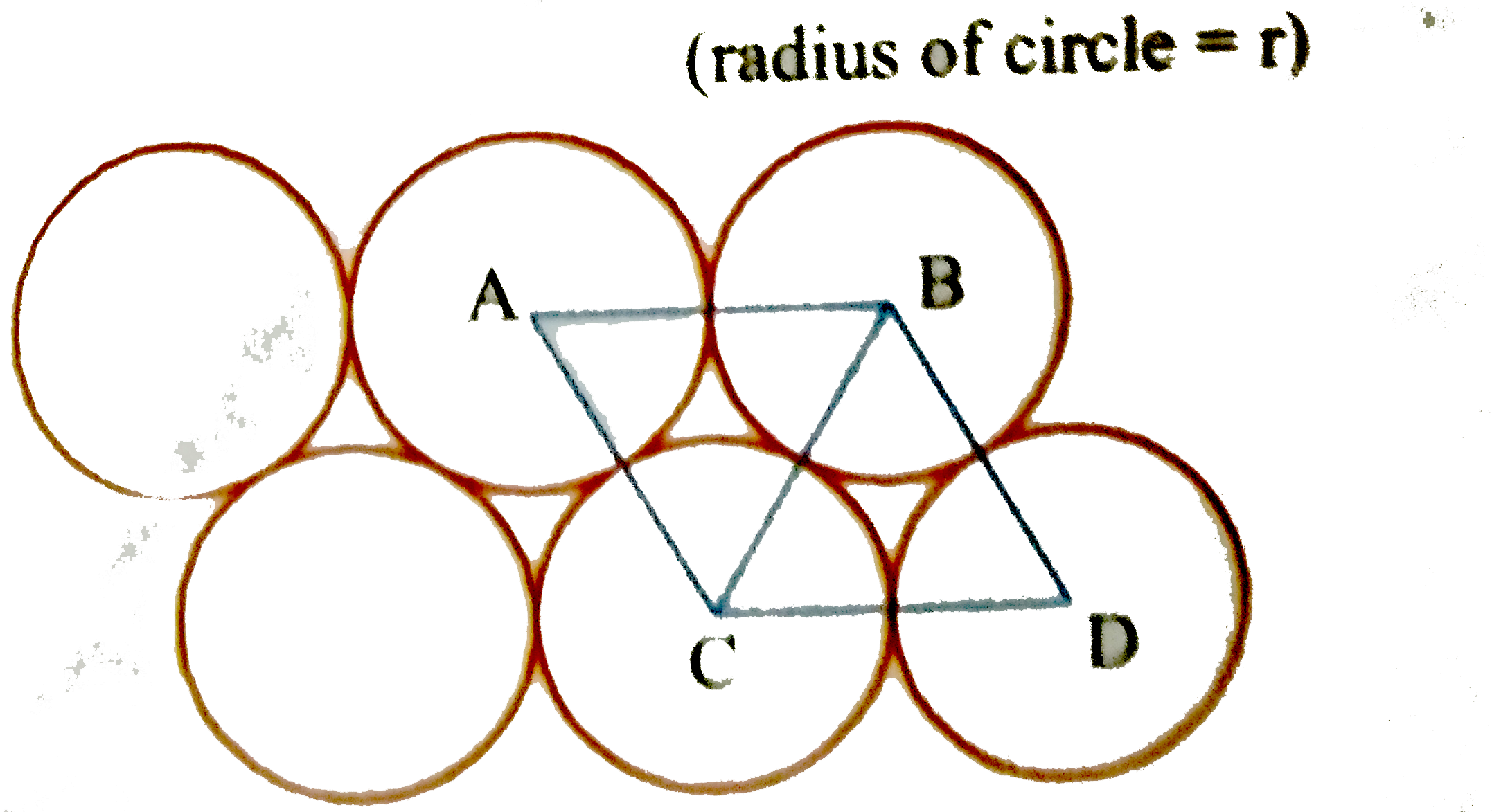
A two dimensional lattice of closest packed identical circles , indicating a suitable unit cell is represent as follows then the fractional void area is
0.93
0.093
0.17
0.017
The correct Answer is:B
Let r be the radius of a circle. The unit cell shown in the figure is composed of two equilateral triangles, ABC and BCD, each with side 2r and s=32r, the area of the unit cell is 2(3r,r3)1/2=2r2√3.
The unit cell contains 16+13+16+13=1 circle of area πr2. The fractional void area is
2r2√3−πr22r2√3=0.093
Similar Questions
Knowledge Check
- Question 1 - Select One
Calculate the void space in a primitive unit cell and also the fraction of the total volume occupied .
A52B48C74D26 - Question 2 - Select One
The packing efficiency of the two dimensional square unit cell shown is :
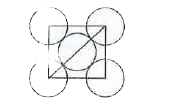 A39.27%B68.02%C74.05%D78.54%
A39.27%B68.02%C74.05%D78.54% - Question 3 - Select One
The packing efficiency of the two dimensional square unit cell shown below is
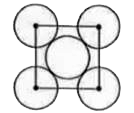 A0.5025B0.6802C0.7405D0.785
A0.5025B0.6802C0.7405D0.785
Consider the parallelotrams shown in the figure below representing two-dimensional cells.
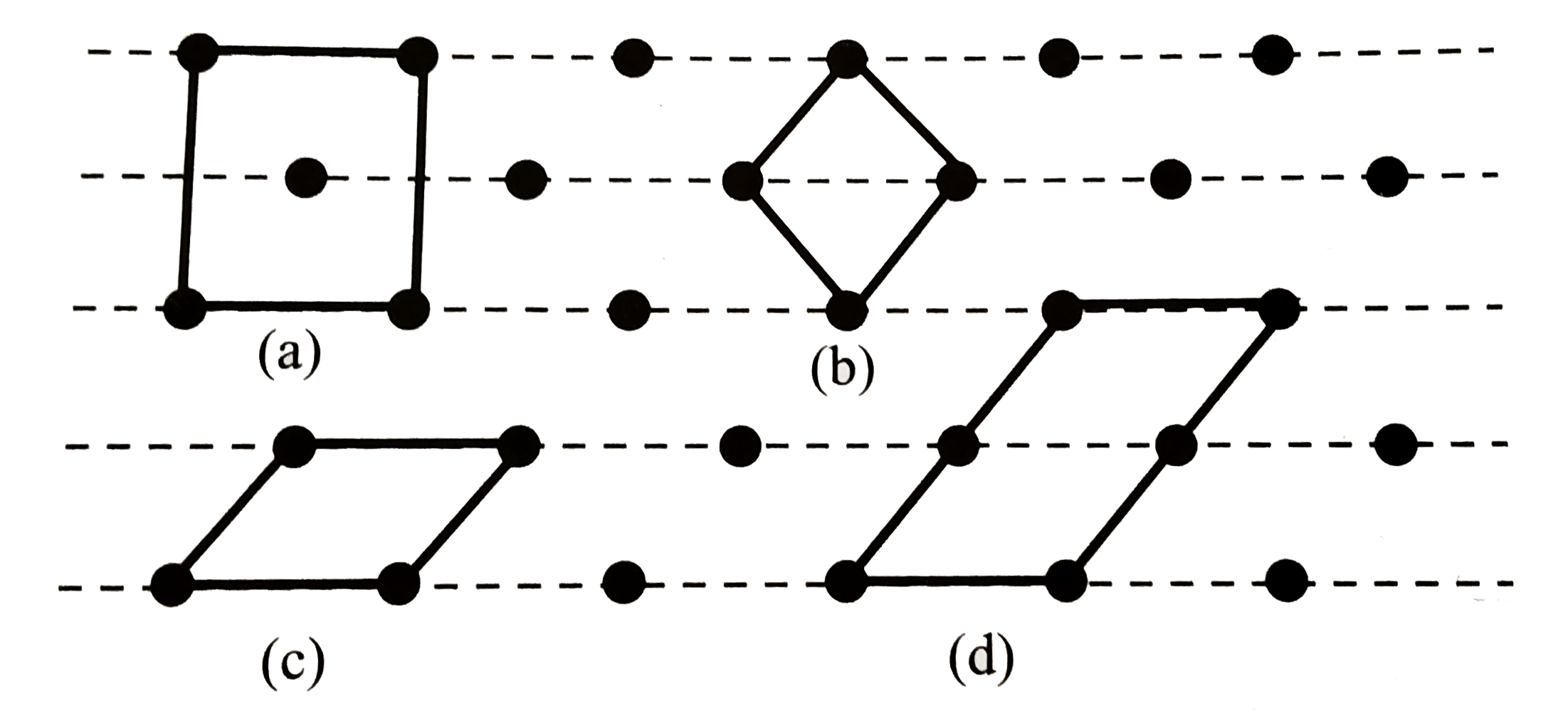
a. Which of these are primitive and which are multiple unit cells? Are any of these orthogonal?
c. What is the relation between the radius of circle and the length of parallelogram for the unit cell shown in the figure below (space filling diagram)?
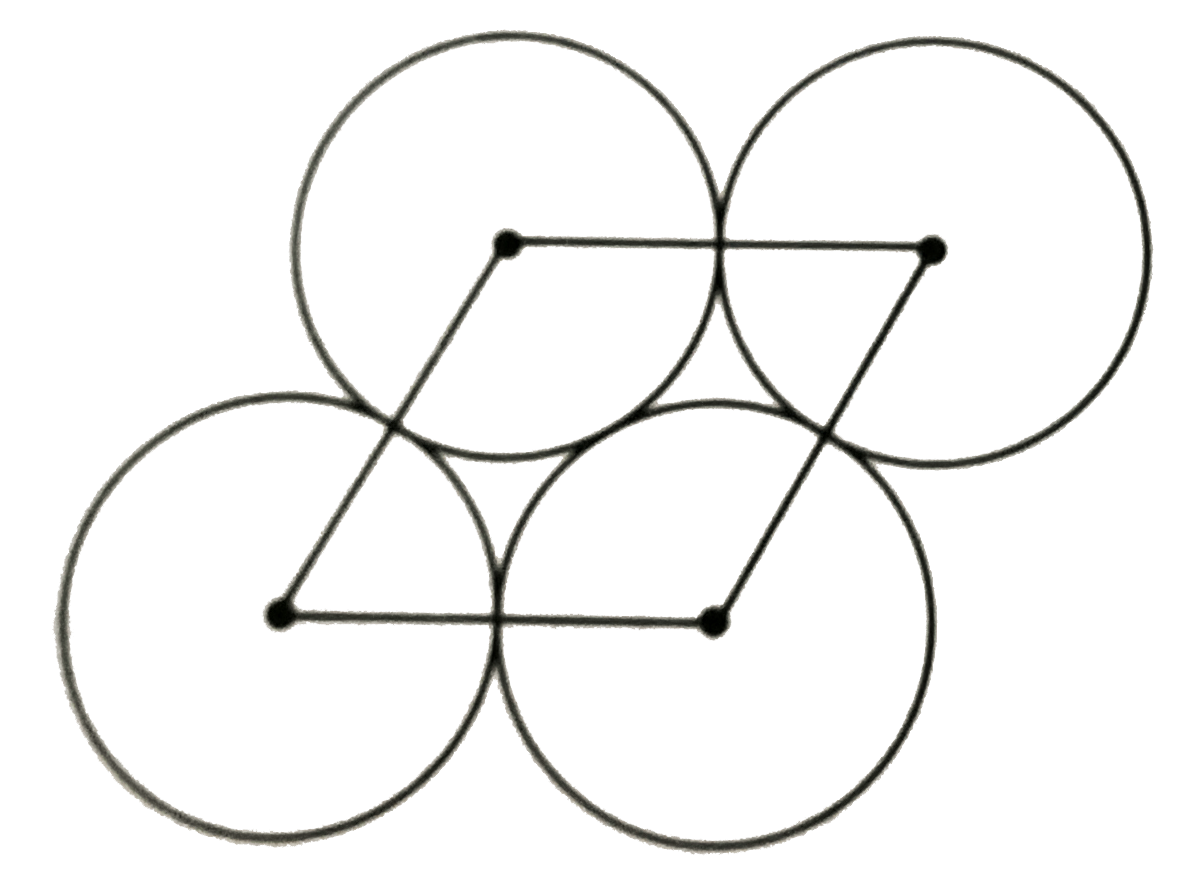
d. How many nearest neighbour circles does a given circle have in the second figure abov?
e. What is the radius of the triangular hole shown in the second figure above?
f. What is the packing fraction of the unit cell in the second figure above?View SolutionA two- dimensional solid is made by alternating circles with radius a and b such that the sides of the circles touch. The packing fraction is defined as the ratio of the are under the circles to the area under the rectangle with sides of the length x and y.
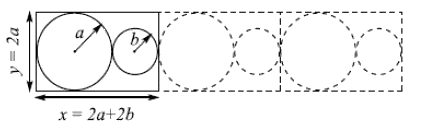
The ratio r = b/a for which the packing fraction is minimized is closed to :View SolutionThe packing efficiency of the two dimensional square unit cell shown below is:
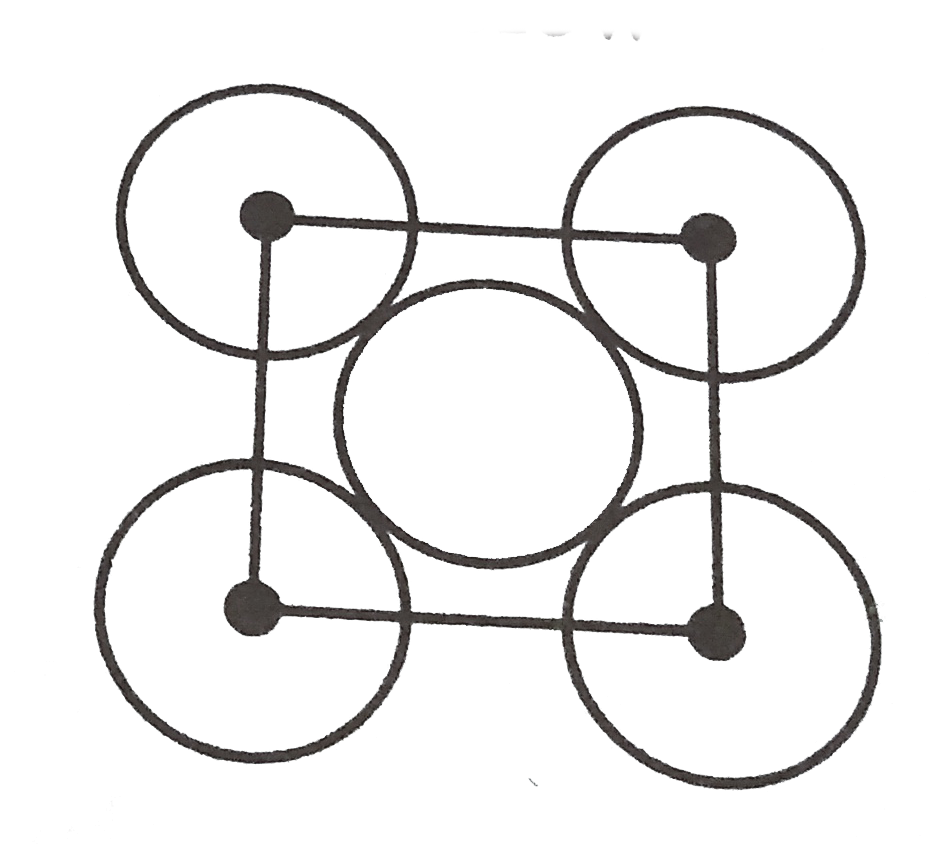 View Solution
View SolutionThe packing fraction of a simple unit cell is ________.
View SolutionConsider the arrangement of circles of equal radii with their centres arranged as per the 2-dimensional lattice defined by a=b,θ=60∘ such that each circle is touching all its nearest neighbours.If all the void areas present are additionally occupied by smmaller circules of relevent size so that the void circles are just contacting their neighbours find the packing efficiency of the configuration in percent.
View Solution

