Iron crystalizes in two bcc lattices, the α− from below 910∘ and the γ-form above 1400∘C, and in an fcc γ-atom between these two temperatures.
What is the symmetry of a face-centered void of a bcc unit cell?
distored octahedral
Linear
Square planer
Tetrahedral
The correct Answer is:A
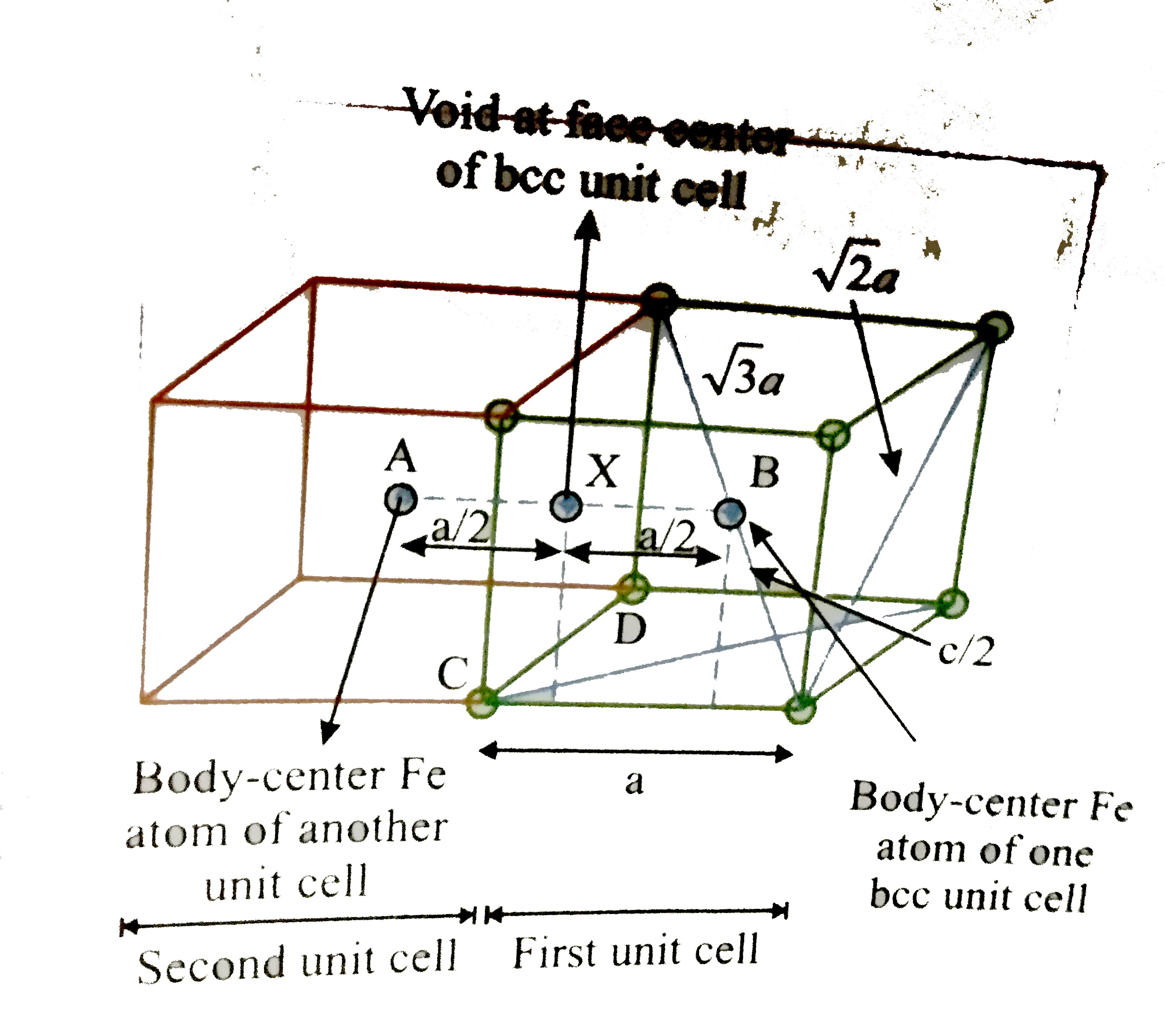
In bcc, the atom at the body center B is in contact with those at the corners, the corner atoms do not touch each other.
The body diagonal =√3a=4r
thus, a=(4√3)r ....(i)
From body center to body center (A-B)=a (figure above) Also, a=2r(Fe)+2r(void)=4r√3
∴rFe+rvoid=2√3r.
∴rvoidrFe=(2√3−1)=0.155
The face diagonal are longer (√2a) than the distance between body centers, so the geometry of the void is a shortened octagedron called distorted octahedron.
Similar Questions
Knowledge Check
Iron crystalizes in two bcc lattices, the α− from below 910∘ and the γ-form above 1400∘C, and in an fcc γ-atom between these two temperatures.
What is the maximum such a void to the host iron ion radius?A0.29B0.1C0.05D0.15Iron crystalizes in two bcc lattices, the α− from below 910∘ and the γ-form above 1400∘C, and in an fcc γ-atom between these two temperatures.
γ-form dissolve appreciable amounts of carbon and occupies ______ in fcc.AT.V.BO.V.CAlternative T.V.Dcubic voidWhat will be the distance between two nearest neighbours in primitive , fcc and bcc unit cell ?
AFor primitive , d=aBFor fcc, d=0.707 aCFor bcc, d=1.732 aDFor bcc , d=1.414 a
What is the number and closest distance between two octahedral voids and two tetrahdral voids in fcc unit cell ?
View SolutionIron crystallizes in several modifications. At about 910∘C, the body centred cubic α - form undergoes a transition to the face centred cubic γ- form. Assuming that the distance between nearest neighbours is same in the two forms at the transition temperature. Calculate the ratio of density of γ - iron to that of α - iron at the transition temperature.
View SolutionIron crystallizes in several modifications. At about 910∘C, the body centred cubic α - form undergoes a transition to the face centred cubic γ- form. Assuming that the distance between nearest neighbours is same in the two forms at the transition temperature. Calculate the ratio of density of γ - iron to that of α - iron at the transition temperature.
View SolutionIron crystallizes in several forms. At 1185 K , the body centred cubic α- form of iron changes to the face centred cubic γ- form of iron. Assuming that the distance betweem the nearest neighbours is the same in two forms at the transition temperature, calcuate the ratio of the density of α- form to that of γ- form at the transition temperature.
View SolutionIron exhibits bcc structure at roomj temperature. Above 900∘C, it transformers to fcc structure. The ratio of density of iron at room temperature to that at 900∘C (assuming molar mass and atomic radius of iron remains constant with temperature) is
View Solution
