Iron exhibits bcc structure at roomj temperature. Above 900∘C, it transformers to fcc structure. The ratio of density of iron at room temperature to that at 900∘C (assuming molar mass and atomic radius of iron remains constant with temperature) is
3√34√2
4√33√2
√3√2
12
The correct Answer is:A
To solve the problem, we need to find the ratio of the density of iron at room temperature (where it has a body-centered cubic (BCC) structure) to the density of iron at 900°C (where it has a face-centered cubic (FCC) structure).
1. Understanding Density Formula:
The density (ρ) of a substance can be expressed using the formula:
ρ=n⋅mNA⋅a3
where:
- n = number of atoms per unit cell
- m = molar mass of the substance
- NA = Avogadro's number
- a = edge length of the unit cell
2. Density at Room Temperature (BCC):
For BCC structure:
- Number of atoms per unit cell (n) = 2
- Relation between edge length (a) and atomic radius (R):
a=4R√3
Therefore, the density of BCC iron at room temperature is:
ρBCC=2⋅mNA⋅(4R√3)3
3. Density at 900°C (FCC):
For FCC structure:
- Number of atoms per unit cell (n) = 4
- Relation between edge length (a) and atomic radius (R):
a=2√2R
Therefore, the density of FCC iron at 900°C is:
ρFCC=4⋅mNA⋅(2√2R)3
4. Calculating the Ratio of Densities:
Now we can find the ratio of the densities:
ρBCCρFCC=2⋅mNA⋅(4R√3)34⋅mNA⋅(2√2R)3
The m and NA cancel out:
=24⋅(2√2R)3(4R√3)3
5. Simplifying the Expression:
- Calculate (2√2R)3=8√2R3
- Calculate (4R√3)3=64R33√3
- Substitute back into the ratio:
=12⋅8√2R364R33√3
- The R3 cancels out:
=12⋅8√2⋅3√364
- Simplifying further:
=12⋅24√664=3√632
6. Final Calculation:
The final ratio of densities is:
ρBCCρFCC=3√632
Final Answer:
The ratio of the density of iron at room temperature to that at 900°C is 3√632.
The density (ρ) of a substance can be expressed using the formula:
ρ=n⋅mNA⋅a3
where:
- n = number of atoms per unit cell
- m = molar mass of the substance
- NA = Avogadro's number
- a = edge length of the unit cell
For BCC structure:
- Number of atoms per unit cell (n) = 2
- Relation between edge length (a) and atomic radius (R):
a=4R√3
Therefore, the density of BCC iron at room temperature is:
ρBCC=2⋅mNA⋅(4R√3)3
For FCC structure:
- Number of atoms per unit cell (n) = 4
- Relation between edge length (a) and atomic radius (R):
a=2√2R
Therefore, the density of FCC iron at 900°C is:
ρFCC=4⋅mNA⋅(2√2R)3
Now we can find the ratio of the densities:
ρBCCρFCC=2⋅mNA⋅(4R√3)34⋅mNA⋅(2√2R)3
The m and NA cancel out:
=24⋅(2√2R)3(4R√3)3
- Calculate (2√2R)3=8√2R3
- Calculate (4R√3)3=64R33√3
- Substitute back into the ratio:
=12⋅8√2R364R33√3
- The R3 cancels out:
=12⋅8√2⋅3√364
- Simplifying further:
=12⋅24√664=3√632
The final ratio of densities is:
ρBCCρFCC=3√632
The ratio of the density of iron at room temperature to that at 900°C is 3√632.
Similar Questions
The temperature at which the root mean squres speed of a gas will be half its value at 0∘C is (assume the pressure remains constant)
View SolutionIn the circuit shown the resistance R is kept in a chamber whose temperature. is 20∘C which remains constant. The initial temperature and resistance of R is 50∘C and 15Ωrespectively. The rate of change of resistance R with temperature is 12Ω/∘C and the rate of decrease of temperature of R is In(3/100) times the temperature difference from the surrounding (Assume the resistance R loses heat only in accordance with Newton's law of cooling) If K is closed at t = 0, then find the
(a) value of. R for which power dissipation in it is maximum.
(b) temperature of R when power dissipation is maximum
(c) time after which the power dissipation will be maximum
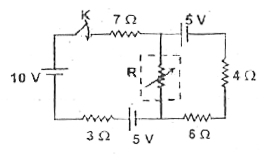
View SolutionWhen heated above 916∘C, iron changes its bcc crystalline from to fcc without the change in the radius of atom . The ratio of density of the crystal before heating and after heating is :
View SolutionAt what temperature will a given mass of a gas occupy a volume of 200L, if it occupies a volume of 260L at a temperature of 30∘C, pressure remaining constant?
View SolutionAir is filled at 60∘C in a vessel of open mouth. The vessel is heated to a temperature T so that 1/4th of air escapes. Assuming the volume of vessel remaining constant, the value of T is
View SolutionAir is filled at 60∘C in a vessel of open mouth. The vessle is heated to a temperature T so that 1/4th of air escapes. Assuming the volume of vessel remaining constant, the value of T is
View SolutionThe γ-form of iron has f structure (edge length 386±) and β-form has b structure (edge length 290±). The ratio of density in γ-form and β-form is
View SolutionThe maximum temperature 1550∘C is obtained in the _____ region of the blast furnace used in the the extraction of iron.
View SolutionWhat is the percentage change in length of 1m iron rod it its temperature changes by 100∘C.α for iron is 2×10−5/∘C.
View SolutionAt what temperature will the speed of sound in hydrogen be the same as in oxygen at 100∘C ? Molar Masses of oxygen and hydrogen are in the ratio 16:1 .
View Solution
