If velocity is given by following function V = x2 . Then find out relation between x & t (assume x = 1 m at t = 0)
Relation between v & x is
v=x2
We know that v=dxdt⇒dxdt=x2
dxx2=dt⇒∫x1dxx2=∫10dt
⇒[−1x]x1=t⇒−1x+1=t
⇒x=11−t
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 1 OBJECTIVE PROBLEMS103videos
KINEMATICS
- BOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 2 OBJECTIVE PROBLEMS75videos
KINEMATICS
- BOOK - MOTIONCHAPTER - HYDROSTATIC, FLUID MECHANICS & VISCOSITYEXERCISE - EXERCISE -3 (SECTION-B) PREVIOUS YEAR PROBLEM7videos
HYDROSTATIC, FLUID MECHANICS & VISCOSITY
- BOOK - MOTIONCHAPTER - KINETIC THEORY OF GASES EXERCISE - EXERCISE-3 SECTION-B16videos
KINETIC THEORY OF GASES
Similar Questions
The acceleration of a particle which is depend on time is given by following function a = 2t + 1 and at time t = 0, x = 1m and ui = 2m/s. Then find out displacement of the particle at t = 3 sec.
View SolutionThe velocity of an object is changing with time and relation is given by the following equation.
v=2t+3t2
Calculate the position of the object from the origin at t = 2 s.
Assume particle to be at origin at t = 0View Solution
Knowledge Check
- Question 1 - Select One
If velocity v varies with time t as v=2t2, then the plot between v and t2 will be given as :
A B
B C
C D
D
- Question 2 - Select One
A particle moves along x− axis. It's velocity is a function of time according to relation V=(3t2−18t+24)m/s assume at t=0 particle is at origin.
Which of the following graph may be correct for the motion of particleA B
B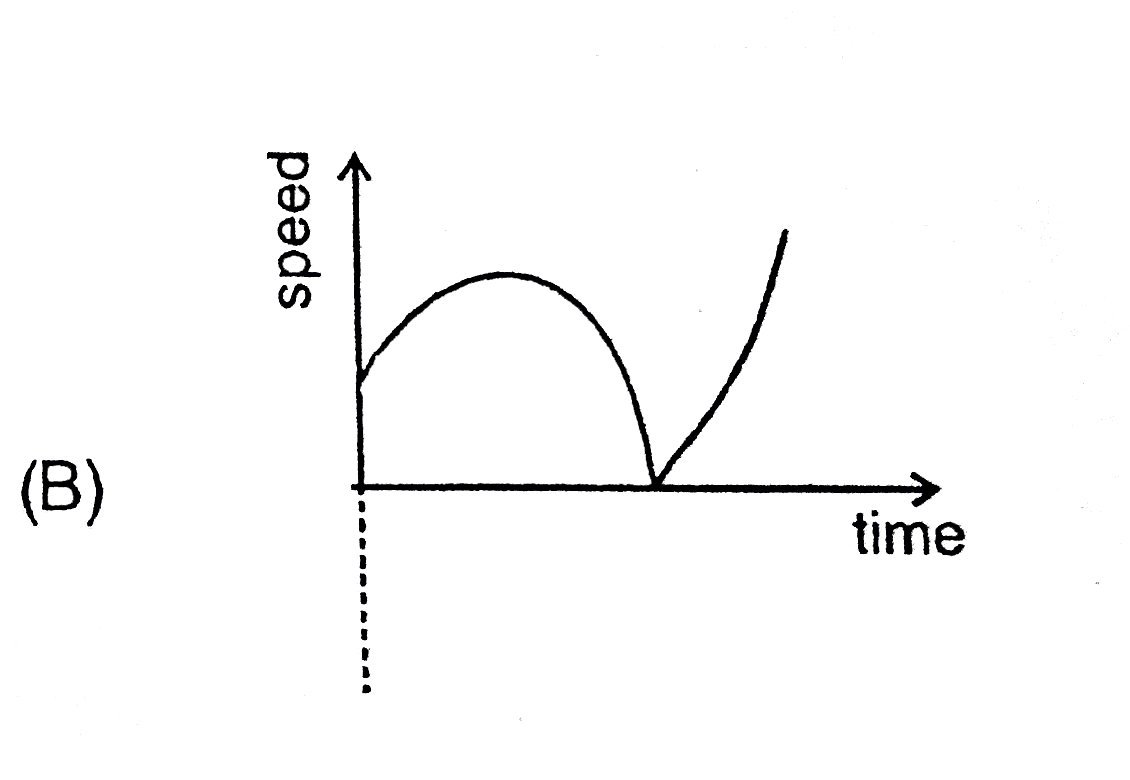 C
C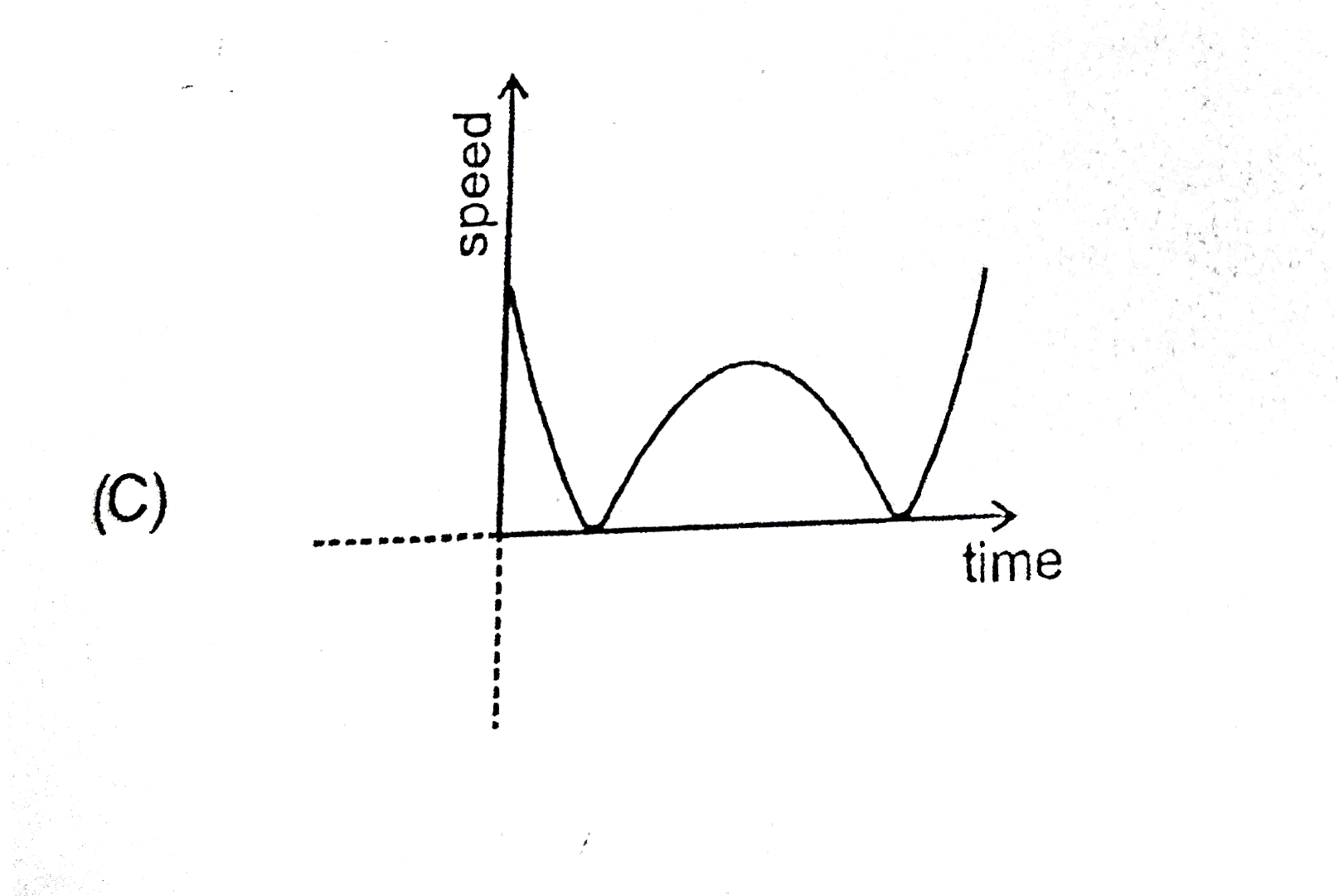 D
D
- Question 3 - Select One
A particle moves along x− axis. It's velocity is a function of time according to relation V=(3t2−18t+24)m/s assume at t=0 particle is at origin.
Distance travelled by particle in 0 to 3 second time interval is :A18mB20mC22mD24m
The displacement x of an object is given as a function of time x=2t+3t2
Calculate the instantaneous velocity of the object at t = 2 sView SolutionA particle moves along x− axis. It's velocity is a function of time according to relation V=(3t2−18t+24)m/s assume at t=0 particle is at origin.
Time interval in which particle speed continuous decreases?View SolutionThe reation between the time t and position x for a particle moving on x-axis is given by t=px2+qx, where p and q are constants. The relation between velocity v and acceleration a is as
View SolutionThe velocity of particle at time t is given by the relation v=6t−t26. The distance traveled in 3 s is, if s=0 at t=0
View SolutionThe intial velocity of a particle moving along x axis is u (at t = 0 and x = 0) and its acceleration a is given by a = kx. Which of the following equation is correct between its velocity (v) and position (x)?
View Solution

