A semicircle of radius R = 5m with diameter AD as shown in figure. Two particles 1 and 2 are at points A and B on shown diameter at t = 0 and move along segments AC and BC with constant speeds u1 and u2 respectively. Then the value of u1u2 for both particles to reach point C simultaneously will be :
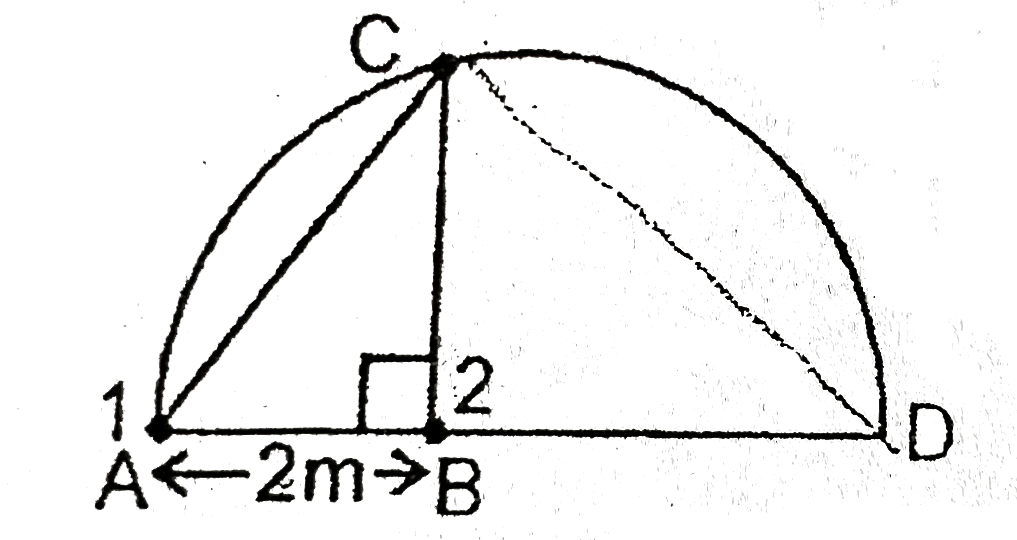
5√24
2√25
2√2
√54
The correct Answer is:D
Step by step video, text & image solution for A semicircle of radius R = 5m with diameter AD as shown in figure. Two particles 1 and 2 are at points A and B on shown diameter at t = 0 and move along segments AC and BC with constant speeds u_(1) and u_(2) respectively. Then the value of (u_(1))/(u_(2)) for both particles to reach point C simultaneously will be : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 2 OBJECTIVE PROBLEMS (Level-2)26videos
KINEMATICS
- BOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 3 SUBJECTIVE PROBLEMS (Level-1)20videos
KINEMATICS
- BOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 1 OBJECTIVE PROBLEMS103videos
KINEMATICS
- BOOK - MOTIONCHAPTER - HYDROSTATIC, FLUID MECHANICS & VISCOSITYEXERCISE - EXERCISE -3 (SECTION-B) PREVIOUS YEAR PROBLEM7videos
HYDROSTATIC, FLUID MECHANICS & VISCOSITY
- BOOK - MOTIONCHAPTER - KINETIC THEORY OF GASES EXERCISE - EXERCISE-3 SECTION-B16videos
KINETIC THEORY OF GASES
Similar Questions
Two bodies A and B are projected simultaneously from points X and Y as shown in the figure, with velocities uA and uB respectively.

Find the ratio of uAuB for both the bodies to collide .View SolutionA body is projectd with the velcity (U1) from the point (A) as shown in Fig. 2. (d). 37. At the same tiem another body uis projected vertcally upwards with the velcoity u2 from the point (B) .What should be the value of u1)/u1 for both the bodies to collide ?
 .View Solution
.View Solution
Knowledge Check
- Question 1 - Select One
Two particles A and B are moving in uniform circular motion in concentric circles of radii rA and rB with speed uA and uB respectively. Their time period of rotation is the same. The ratio of angular speed of a to that of B will be:
A1:1BrA:rBCυA:υBDrB:rA - Question 2 - Select One
Two particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
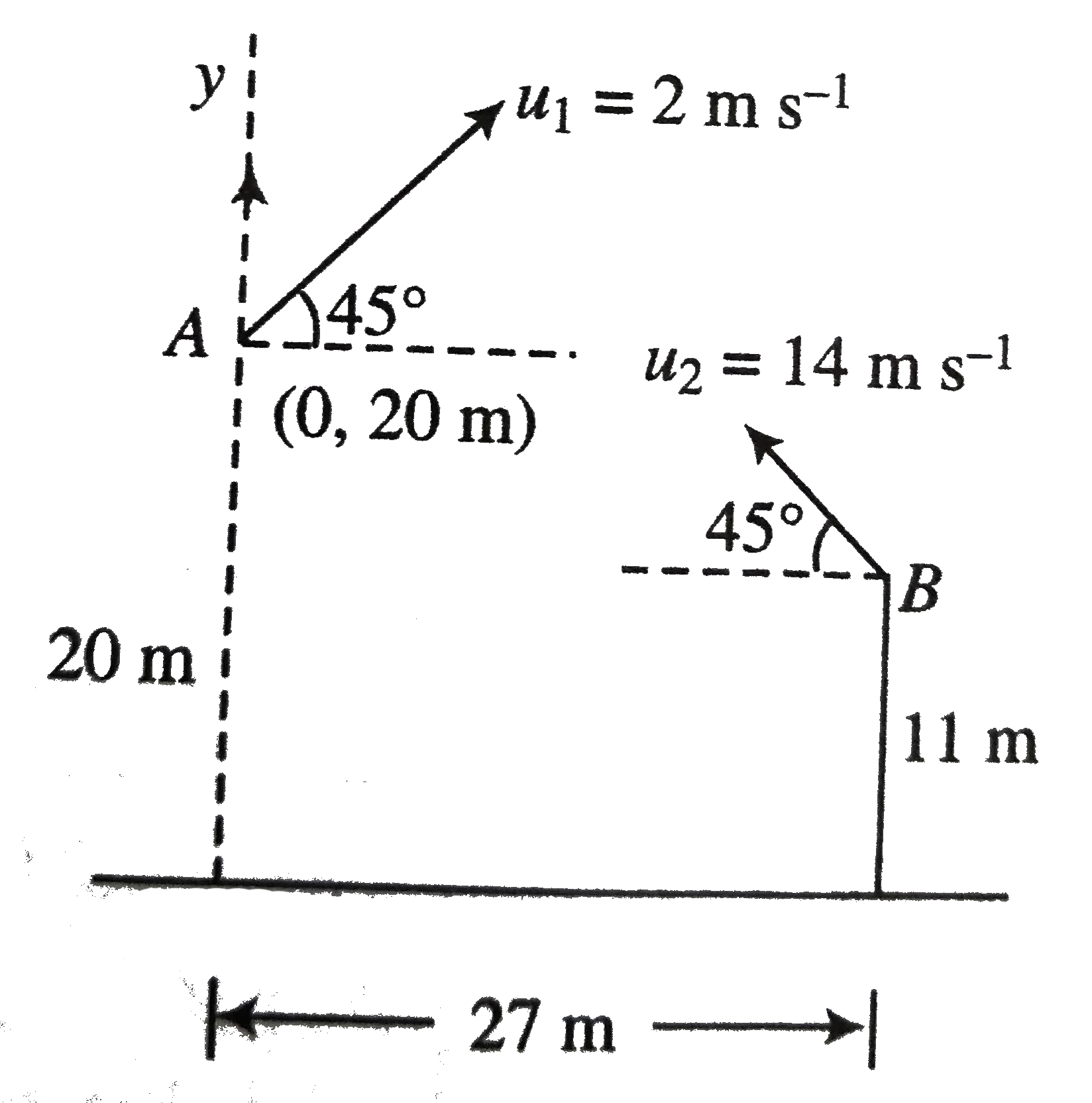
The relative velocity of B as seen from A inA−8√2ˆi+6(√2)ˆjB4√2ˆi+3(√3)ˆjC3√5ˆi+2(√3)ˆjD3√2ˆi+4(√3)ˆj - Question 3 - Select One
The lateral magnification of the lens with an object located at two different position u1 and u2 are m1 and m2 , respectively. Then the focal length of the lens is
Af=√m1m2(μ2−μ1)Bf=√m1m2(u2−u1)C(u2−u1)√m1m2D(u2−u1)(m2)−1−(m1)−1
As shown in Fig. 5.29, a body is projected with velocity u1 from the point A. At the same time another body is projected vertically upwards with velocity u2 from the point B. What should be the value of u1/u2 for both the bodies to collide ?
 View Solution
View SolutionTwo path 1 and 2 are shown in figure. If the change in internal energies are U1, and U2 for path 1 and 2 respectively, then
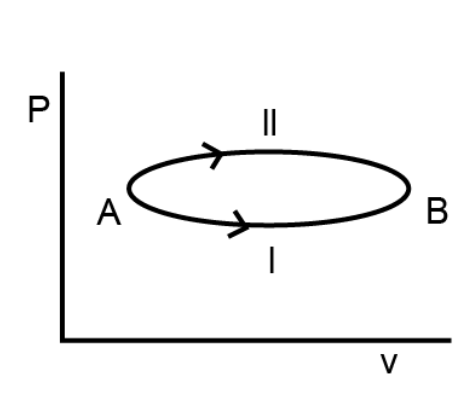 View Solution
View SolutionIn the arrangement shown in figure if speed of point 1 and point 2 are u, then what is the velocity of block at given instant of time.
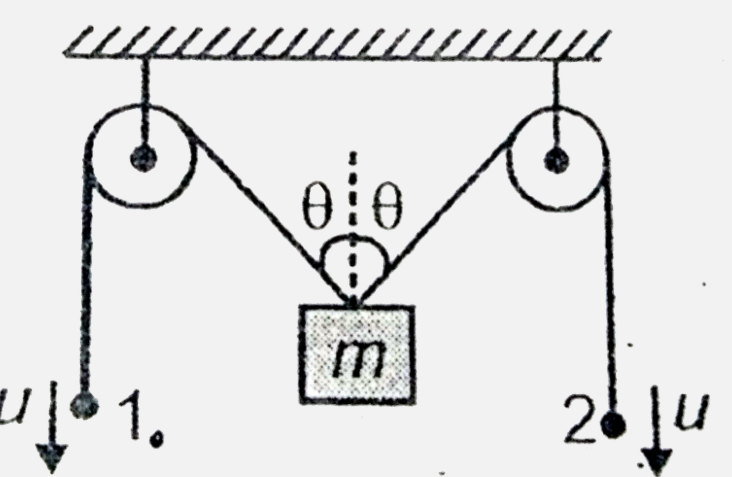 View Solution
View SolutionFor a diatomic gas change in internal energy for unit change in temperature for constant pressure and constant volume is ΔU1 and ΔU2 respectively. The ratio of ΔU1:ΔU2 is
View SolutionA particle P is moving in a circle of radius r with a uniform speed u. C is the centre of the circle and AB is diameter. The angular velocity of P about A and V are in the ratio :
View Solution

