A balloon is moving vertically upward with constant acceleration (g/2) in upward direction Particle 'A' was dropped from the balloon and 2 sec later another particle 'B' was dropped from the same balloon. Assume that motion of the balloon remains unaffected. Find the separation distance between 'A' and 'B', 6 sec after dropping the particle 'B'. None of the particles reaches the ground during the time interval under consideration (g=10 m/ )
To solve the problem, we will analyze the motion of both particles A and B dropped from the balloon, which is moving upward with a constant acceleration of g2 (where g=10m/s2).
1. Determine the Balloon's Motion:
- The balloon is moving upward with an acceleration of g2=102=5m/s2.
- The initial velocity of the balloon is u (which we will assume is unknown for now).
2. Calculate the Velocity of the Balloon at the Time of Dropping Particle A:
- When particle A is dropped, it has the same upward velocity as the balloon.
- The time taken for the balloon to reach the moment A is dropped is tA=0 seconds.
3. Calculate the Velocity of the Balloon After 2 Seconds:
- The velocity of the balloon after 2 seconds can be calculated using the equation:
v=u+at=u+(g2)⋅2=u+5m/s
4. Determine the Motion of Particle A:
- Particle A is dropped from the balloon at t=0 seconds. Its initial velocity is vA=u+5m/s (upward).
- The acceleration acting on A is −g=−10m/s2 (downward).
- The position of particle A after t seconds can be given by:
sA=vAt−12gt2=(u+5)t−5t2
5. Determine the Motion of Particle B:
- Particle B is dropped 2 seconds after A, so it is dropped at t=2 seconds.
- At the moment B is dropped, the balloon's velocity is vB=u+5+5⋅2=u+15m/s.
- The position of particle B after t seconds (where t is measured from the moment B is dropped) is:
sB=vB(t−2)−12g(t−2)2=(u+15)(t−2)−5(t−2)2
6. Find the Separation Between A and B After 6 Seconds:
- At t=6 seconds, particle A has been falling for 6 seconds, and particle B has been falling for 4 seconds.
- The position of A at t=6:
sA=(u+5)⋅6−5⋅62=6u+30−180=6u−150
- The position of B at t=6:
sB=(u+15)(6−2)−5(6−2)2=(u+15)⋅4−5⋅16=4u+60−80=4u−20
7. Calculate the Separation:
- The separation d between A and B at t=6 seconds is:
d=sA−sB=(6u−150)−(4u−20)=6u−150−4u+20=2u−130
8. Substituting Values:
- Since we do not know the initial velocity u, we can express the separation in terms of u. However, we can also assume u=0 (for simplicity), which gives:
d=2(0)−130=−130 m(indicating that A is 130 m below B)
Final Separation Calculation:
- The final separation distance between particles A and B after 6 seconds is 130m.
- The balloon is moving upward with an acceleration of g2=102=5m/s2.
- The initial velocity of the balloon is u (which we will assume is unknown for now).
- When particle A is dropped, it has the same upward velocity as the balloon.
- The time taken for the balloon to reach the moment A is dropped is tA=0 seconds.
- The velocity of the balloon after 2 seconds can be calculated using the equation:
v=u+at=u+(g2)⋅2=u+5m/s
- Particle A is dropped from the balloon at t=0 seconds. Its initial velocity is vA=u+5m/s (upward).
- The acceleration acting on A is −g=−10m/s2 (downward).
- The position of particle A after t seconds can be given by:
sA=vAt−12gt2=(u+5)t−5t2
- Particle B is dropped 2 seconds after A, so it is dropped at t=2 seconds.
- At the moment B is dropped, the balloon's velocity is vB=u+5+5⋅2=u+15m/s.
- The position of particle B after t seconds (where t is measured from the moment B is dropped) is:
sB=vB(t−2)−12g(t−2)2=(u+15)(t−2)−5(t−2)2
- At t=6 seconds, particle A has been falling for 6 seconds, and particle B has been falling for 4 seconds.
- The position of A at t=6:
sA=(u+5)⋅6−5⋅62=6u+30−180=6u−150
- The position of B at t=6:
sB=(u+15)(6−2)−5(6−2)2=(u+15)⋅4−5⋅16=4u+60−80=4u−20
- The separation d between A and B at t=6 seconds is:
d=sA−sB=(6u−150)−(4u−20)=6u−150−4u+20=2u−130
- Since we do not know the initial velocity u, we can express the separation in terms of u. However, we can also assume u=0 (for simplicity), which gives:
d=2(0)−130=−130 m(indicating that A is 130 m below B)
- The final separation distance between particles A and B after 6 seconds is 130m.
Topper's Solved these Questions
- KINEMATICSBOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 4 PREVIOUS YEAR (LEVEL 1)
22 Videos
- KINEMATICSBOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 4 PREVIOUS YEAR (LEVEL 2)
6 Videos
- KINEMATICSBOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 3 SUBJECTIVE PROBLEMS (Level-1)
20 Videos
- HYDROSTATIC, FLUID MECHANICS & VISCOSITYBOOK - MOTIONCHAPTER - HYDROSTATIC, FLUID MECHANICS & VISCOSITYEXERCISE - EXERCISE -3 (SECTION-B) PREVIOUS YEAR PROBLEM
7 Videos
- KINETIC THEORY OF GASES BOOK - MOTIONCHAPTER - KINETIC THEORY OF GASES EXERCISE - EXERCISE-3 SECTION-B
16 Videos
Similar Questions
A balloon starts from the state of rest from the ground with constant acceleration g/n. after time T, a stone is dropped from the balloon. If stone takes time T to reach the ground then calculate value of n.
View SolutionA balloon is rising vertically upwards with uniform acceleration 15.7m/s2 .A stone is dropped from it. After 4s another stone is dropped from it.Find the distance between the two stones 6 second after the second stone is dropped.
View Solution
Knowledge Check
A balloon is rising vertically upwards with uniform acceleration 15.7m/s2 .A stone is dropped from it. After 4s another stone is dropped from it.Find the distance between the two stones 6 second after the second stone is dropped.
A616 mB716 m.C816 mDNone of theseFrom a balloon rising vertically with uniform acceleration f a ball is dropped, 4 seconds after this another ball is dropped from the balloon. The distance. between the two balls 2 seconds after the second ball is dropped is
A16 (g+f)B10 (g+f)C8 (g+f)DNoneA particle is dropped from a height 12 g metre and 4 s after another particle is projected from the ground towards it with a velocity 4gms−1 The time after which the second particle meets first is
A4 sB2 sC12sD1 s
A balloon starts rising upwards with constant acceleration a and afrer time t0, second, a packet is dropped from it which reaches the ground aftre t seconds of dropping . Derermine the value of t
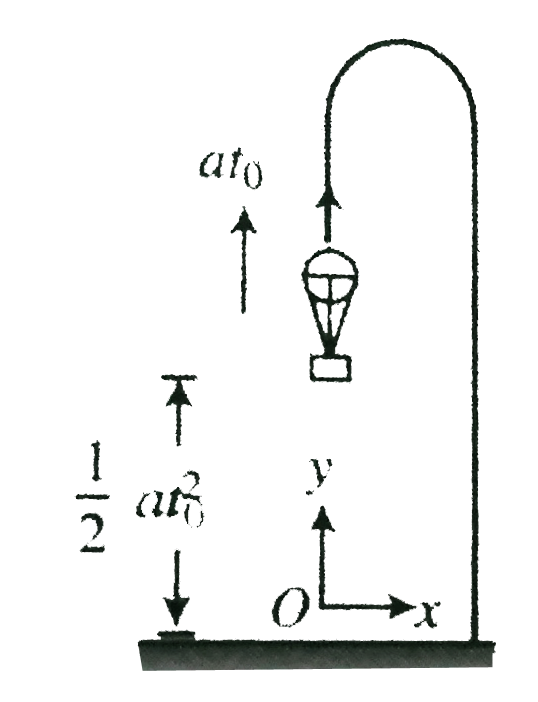 .
.
View SolutionA balloon in ascending vertically with an acceleration of 1ms−2. Two stones are dropped from it at an interval of 2s. Find the distance berween them 1.5s after the second stone is released.
View SolutionA bolloon starts from rest moves vertically upwards with an acceleration g/8ms−2 a stone falls from the balloon after 8 s from the start. Further time taken by the stone to reachg the ground (g=9.8ms−2) is
View SolutionA balloon reses from rest on the ground with constant acceleration g//8. A stone is dropped from the balloon when the balloon has resen to a height of (H). Find the time taken by the stone to reach the ground.
View SolutionA particle is dropped from a height 12 g metre and 4 s after another particle is projected from the ground towards it with a velocity 4gms−1 The time after which the second particle meets first is
View Solution
