A: If the transformed equation of a curve is 9X2+16Y2=144 when the axes are rotated through an angle 45∘, then the original equation is 25x2−14xy+25y2=288.
R: If f(x,y)=0 is the transformed equation of a curve when the axes are rotate through an angle θ then the original equation of the curve is f(xcosθ+ysinθ,−xsinθ+ycosθ)=0Solution in Telugu
Both A and R are true and R is the correct explanation of A.
Both A and R are true but R is not the correct explanation of A.
A is true but R is false
A is false but R is false
The correct Answer is:A
Step by step video, text & image solution for A: If the transformed equation of a curve is 9X^(2) + 16Y^(2) = 144 when the axes are rotated through an angle 45^(@), then the original equation is 25x^(2) - 14xy+ 25y^(2) = 288. R: If f(x,y)=0 is the transformed equation of a curve when the axes are rotate through an angle theta then the original equation of the curve is f(x cos theta + y sin theta, -x sin theta + y cos theta)=0 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - TRANSFORMATION OF AXES EXERCISE - SET-32videos
TRANSFORMATION OF AXES
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - THEORY OF EQUATIONSEXERCISE - SET - 44videos
THEORY OF EQUATIONS
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - TRIGONOMETRIC EQUATIONS EXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) SET - 44videos
TRIGONOMETRIC EQUATIONS
Similar Questions
To remove the first degree terms in the following equation origin should be shifted to the another point then calculate the new origins is
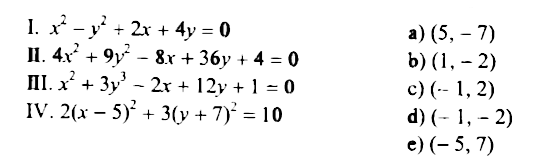 03:21View Solution
03:21View SolutionA : the equation whose roots are multiplied by 2 of those of x5−2x4+3x3−2x2+4x+3=0 is x5−4x4+12x3−16x2+64x+96=0.
R: the equation whose roots are multiplied by k of those of f(x) = 0 is f(x/k) = 0.02:04View SolutionA : The general solution of sinx=−1 is nπ+(−1)n3π2,n∈Z
R : The principal solution of sin x = 0 lies in [−π/2,π/2]06:21View SolutionThe transformed equation of curve x^(2)+2sqrt(3)xy-y^(2)-8=0, when the axes are rotated through an angle (pi)/(6) is
07:01View SolutionThe transformed equation of x^(2)+y^(2)=r^(2) when the axes are rotated through an angle 36^(@) is
03:26View SolutionWhen the axes are rotated through an angle 45∘, the transformed equation of a curve is 17x2−16xy+17y2=225. Find the original equation of the curve.
05:56View SolutionThe transformed equation of x2+y2=r2 when the axes are rotated through an angle 36∘ is
04:59View SolutionIf the axes are rotated through, an angle θ, the transformed equation of x2+y2=25 is
04:29View SolutionIf the transformed equation of a curve is 17x2−16xy+17y2=225 when the axes are rotated through an angle 45∘, then the original equation of the curve is
05:50View SolutionIf the equation of a curve C is transformed to 9x2+25y2=225 be the rotation of the coordinate axes about the origin through an angle π4 in the positive direction then the equation of the curve C, before the transformation is
04:28View SolutionWhen the axes are rotated through an angle 45∘, the transformed equation of a curve is 17x2−16xy+17y2=225. Find the original equation of the curve.
03:52View SolutionIf the transformed equation of a curve is X2+2√3XY−Y2=2a2 ,when the axes are rotated through an angle of 60∘ ,then the original equation
06:18View SolutionIf the transformed equation of a curve is X2+2√3XY−Y2=2a2 when the axes are rotated through angle 600, then find the original equation of the curve.
03:54View SolutionThe transformed equation of x2+y2=r2 when the axes rotated through an angle 36∘ is
05:08View SolutionIf the transformed equation of a curve is X2−2XYtan2α−Y2=a2 when the axes are rotated through an angle α , then the original equation of the curve is
03:32View Solution

