A charge is uniformly distributed inside a spherical body of radius r1=2r0 having a concetric cavity of radius r2=r0 (ρ is charge density inside the sphere). The potential of a point P at a distance 3r02 from the centre is
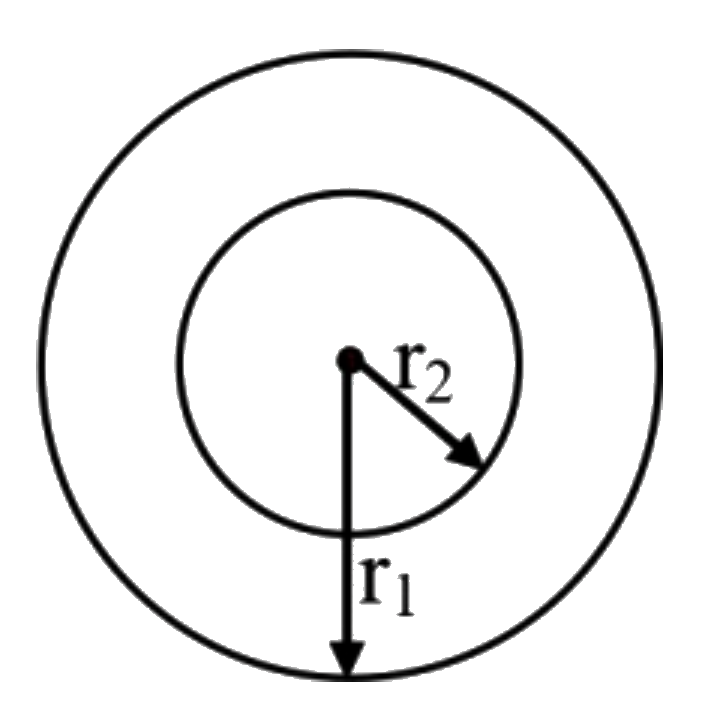
7ρr206ε0
101ρr2072ε0
17ρr2072ε0
none of these
The correct Answer is:B
Step by step video, text & image solution for A charge is uniformly distributed inside a spherical body of radius r_(1) = 2 r_(0) having a concetric cavity of radius r_(2) = r_(0) (rho is charge density inside the sphere). The potential of a point P at a distance (3 r_0)/(2) from the centre is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
A11GMmR2B14GMmR2CGMm2R2DGMmR2 - Question 2 - Select One
A hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
Adecreases as r increases for r<R and r>RBincreases as r increases for r<R and r>RCzero as r increases for r<R, decreases as r increases for r>RDzero as r increases for r<R, increases for r>R - Question 3 - Select One
Let a total charge 2Q be distributed in a sphere of radius R, with the charge density given by , ρ(r)=kr, where r is the distance from the centre. Two charge A and B, of –Q each, are placed on diametrically opposite points, at equal distance, a from the centre. If A and B do not experience any force, then:
Aa=2−1/4RBa=R√3Ca=8−1/4RDa=3R21/4
A sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.
 View Solution
View SolutionA solid sphere having uniform charge density ρ and radius R is shown in figure. A spherical cavity ofradius R2 is made in it. What is the potential at point O?
 View Solution
View SolutionA charge q is uniformly distributed over the volume of a shpere of radius R. Assuming the permittively to be equal to unity throughout, find the potential
(a) at the centre of the sphere,
(b) inside the sphere as a function of the distance r from its centre.View SolutionElectric charge q is uniformly distributed in a spherical space from which a cavity of diameter equal to the radius R of the spherical space has been removed. Calculate the potential and field at a point P lying on the diameter of the cavity at a distance r>r/2 but lt R from the centre of the sphere.
View SolutionA sphere of radius R contains charge density ρ(r)=A(R−r), for 0<r<R. The total electric charge inside the sphere is Q.
The value of A in terms of Q and R isView Solution

