Electric charge q is uniformly distributed in a spherical space from which a cavity of diameter equal to the radius R of the spherical space has been removed. Calculate the potential and field at a point P lying on the diameter of the cavity at a distance but lt R from the centre of the sphere.
The correct Answer is:
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENIALBOOK - NN GHOSHCHAPTER - ELECTRIC FIELD AND POTENIALEXERCISE - EXERCISE
21 Videos
- DYNAMO, MOTOR, TRANSFORMERBOOK - NN GHOSHCHAPTER - DYNAMO, MOTOR, TRANSFORMEREXERCISE - EXERCISE
8 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NN GHOSHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERICISES-B
18 Videos
Similar Questions
A solid spherical region, having a spherical cavity whose diameter R is equal to the radius of the spherical region, has a total charge Q. Find the electric field at a point P as shown in figure
 .
.
View SolutionA solid spherical region having a spherical cavity whose daimeter R is equal to the radius of the spherical region, has a total charge 'Q'. Find the electric field and potential at a point P as shown.

View Solution
Knowledge Check
A solid spherical region, having a spherical cavity whose diameter R is equal to the radius of the spherical region, has a total charge Q. Find the electric field at a point P as shown in figure
 .AQ18πε0⎡⎢ ⎢ ⎢⎣4x2−1(x−R2)2⎤⎥ ⎥ ⎥⎦BQ28πε0⎡⎢ ⎢ ⎢⎣8x2−1(x−R2)2⎤⎥ ⎥ ⎥⎦CQ28πε0[8x2−1(x−R)2]DQ18πε0[4x2−1(x−R)2]
.AQ18πε0⎡⎢ ⎢ ⎢⎣4x2−1(x−R2)2⎤⎥ ⎥ ⎥⎦BQ28πε0⎡⎢ ⎢ ⎢⎣8x2−1(x−R2)2⎤⎥ ⎥ ⎥⎦CQ28πε0[8x2−1(x−R)2]DQ18πε0[4x2−1(x−R)2]The electric field at a distance 3R/2 from the centre of a charge conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
AE2BzeroCEDE4A charge is uniformly distributed inside a spherical body of radius r1=2r0 having a concetric cavity of radius r2=r0 (ρ is charge density inside the sphere). The potential of a point P at a distance 3r02 from the centre is
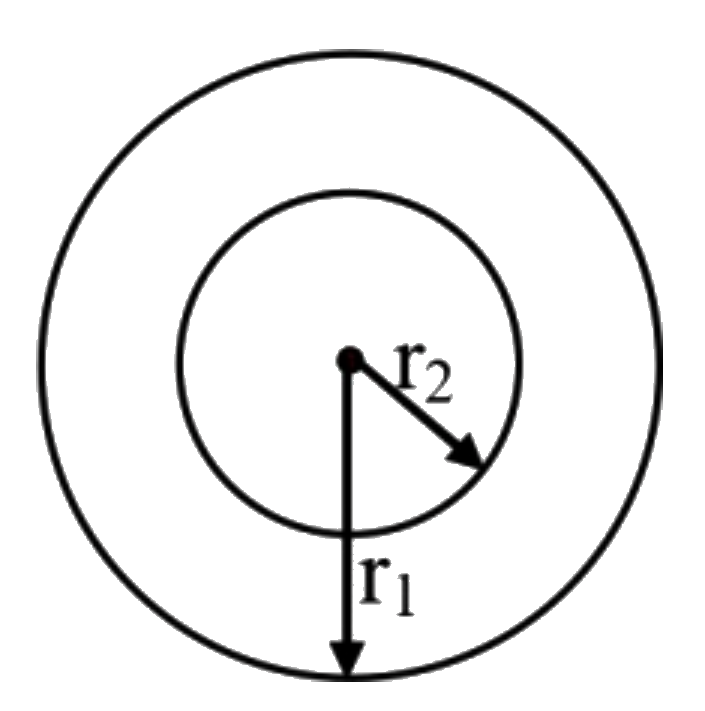 A7ρr206ε0B101ρr2072ε0C17ρr2072ε0Dnone of these
A7ρr206ε0B101ρr2072ε0C17ρr2072ε0Dnone of these
The electric field at a distance 3R/2 from the centre of a charge conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
View SolutionThe electric field at a distance 3R/2 from the centre of a charge conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
View SolutionA charge is uniformly distributed inside a spherical body of radius r1=2r0 having a concetric cavity of radius r2=r0 (ρ is charge density inside the sphere). The potential of a point P at a distance 3r02 from the centre is

View SolutionIf the potential at the centre of a uniformly charged hollow sphere of radus R is V, then electric field at a distance r from the centre of sphere will be (r>R).

View SolutionThe electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre
View Solution
