If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord. Solution in Kannada
Step by step video & image solution for If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLESBOOK - SUBHASH PUBLICATIONCHAPTER - CIRCLESEXERCISE - EXERCISE 12.5
12 Videos
- CIRCLESBOOK - SUBHASH PUBLICATIONCHAPTER - CIRCLESEXERCISE - EXERCISE 12.6
7 Videos
- CIRCLESBOOK - SUBHASH PUBLICATIONCHAPTER - CIRCLESEXERCISE - EXERCISE 12.1
2 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - SUBHASH PUBLICATIONCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE 11.4
3 Videos
- CO-ORDINATE GEOMETRY BOOK - SUBHASH PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - EXERCISE 9.3
1 Videos
Similar Questions
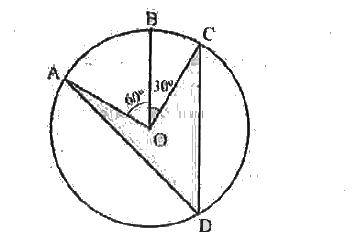
In Fig. 12.36 A, B and C are three points on a circle with centre O such that BOC=30∘andAOB=60∘. If D is a point on the circle other than the arc ABC, find ADC.
View SolutionProve that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
View SolutionSuppose you are given a circle. Give a construction to find its centre.
View SolutionParallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
View SolutionIn which quandrant or on which axis do each of the points (−2,4),(3,−1),(−1,0),(1,2)and(−3,−5) lie ? Verify you answer by locating them on the cartesian plane.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments ofone chord are equal to corresponding segments of the other chord.
View SolutionIf two equal chords of a circle in intersect within the circle, prove that : the segments of the chord are equal to the corresponding segments of the other chord. the line joining the point of intersection to the centre makes equal angles with the chords.
View SolutionIf two equal chords of a circle in intersect within the circle, prove that: the segments of the chord are equal to the corresponding segments of the other chord. the line joining the point of intersection to the centre makes equal angles with the chords.
View SolutionIf two chords of a circle intersect inside or outside the circle when produced ; the rectangle formed by the two segments of one chord is equal in area to the rectangle formed by the two segments of the other chord.
View Solutionयदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर प्रतिच्छेद करें, तो सिद्ध कीजिए कि एक जीवा के खण्ड दूसरी जीवा के संगत खण्डों के बराबर हैं |
View Solutionयदि एक वृत्त की दो समान लम्बाई की जिवाएँ वृत्त के अंदर प्रतिच्छेद करती हो, तो सिध्द करो कि :
(i) एक जीवा के खंड दूसरी जीवा के संगत खंडो के बराबर होते है ।
(ii) प्रतिच्छेद बिन्दु को केंद्र से मिलाने वाली रेखा, जीवाओ से बराबर कोण बनाती है ।
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
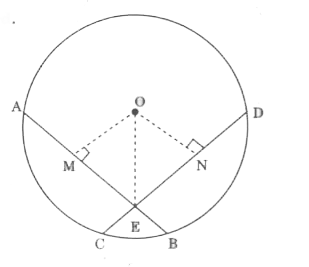
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
View SolutionIf two equal chords of a circle in intersect within the circle, prove that : the segments of the chord are equal to the corresponding segments of the other chord. the line joining the point of intersection to the centre makes equal angles with the chords.
View Solution
