If two chords of a circle intersect inside or outside the circle when produced ; the rectangle formed by the two segments of one chord is equal in area to the rectangle formed by the two segments of the other chord.
To solve the problem, we need to understand the relationship between the segments of the chords that intersect either inside or outside the circle. Let's break down the solution step by step.
Step 1: Understand the Chords
Let’s denote the two chords as AB and CD. These chords intersect at a point P, which can be either inside or outside the circle.
Step 2: Identify the Segments
When the chords intersect, we can identify the segments formed by the intersection:
- For chord AB, the segments are AP and PB.
- For chord CD, the segments are CP and PD.
Step 3: Write the Relationship
According to the property of intersecting chords, the product of the lengths of the segments of one chord is equal to the product of the lengths of the segments of the other chord. This can be expressed mathematically as:
AP×PB=CP×PD
Step 4: Formulate the Rectangles
From the segments identified:
- The rectangle formed by the segments of chord AB is given by the area AP×PB.
- The rectangle formed by the segments of chord CD is given by the area CP×PD.
Step 5: Conclude the Equality
From the relationship established in Step 3, we conclude that:
AP×PB=CP×PD
This shows that the area of the rectangle formed by the segments of chord AB is equal to the area of the rectangle formed by the segments of chord CD.
Final Statement
Thus, we have proven that if two chords of a circle intersect either inside or outside the circle, the rectangle formed by the two segments of one chord is equal in area to the rectangle formed by the two segments of the other chord.
---
Let’s denote the two chords as AB and CD. These chords intersect at a point P, which can be either inside or outside the circle.
When the chords intersect, we can identify the segments formed by the intersection:
- For chord AB, the segments are AP and PB.
- For chord CD, the segments are CP and PD.
According to the property of intersecting chords, the product of the lengths of the segments of one chord is equal to the product of the lengths of the segments of the other chord. This can be expressed mathematically as:
AP×PB=CP×PD
From the segments identified:
- The rectangle formed by the segments of chord AB is given by the area AP×PB.
- The rectangle formed by the segments of chord CD is given by the area CP×PD.
From the relationship established in Step 3, we conclude that:
AP×PB=CP×PD
This shows that the area of the rectangle formed by the segments of chord AB is equal to the area of the rectangle formed by the segments of chord CD.
Thus, we have proven that if two chords of a circle intersect either inside or outside the circle, the rectangle formed by the two segments of one chord is equal in area to the rectangle formed by the two segments of the other chord.
Similar Questions
Theorem of internal division of chords.
Suppose two chords of a circle intersect each other in the interior of the circle, then the product of the lengths of the two segments of one chord is equal to the product of the lengths of the two segments of the other chord.
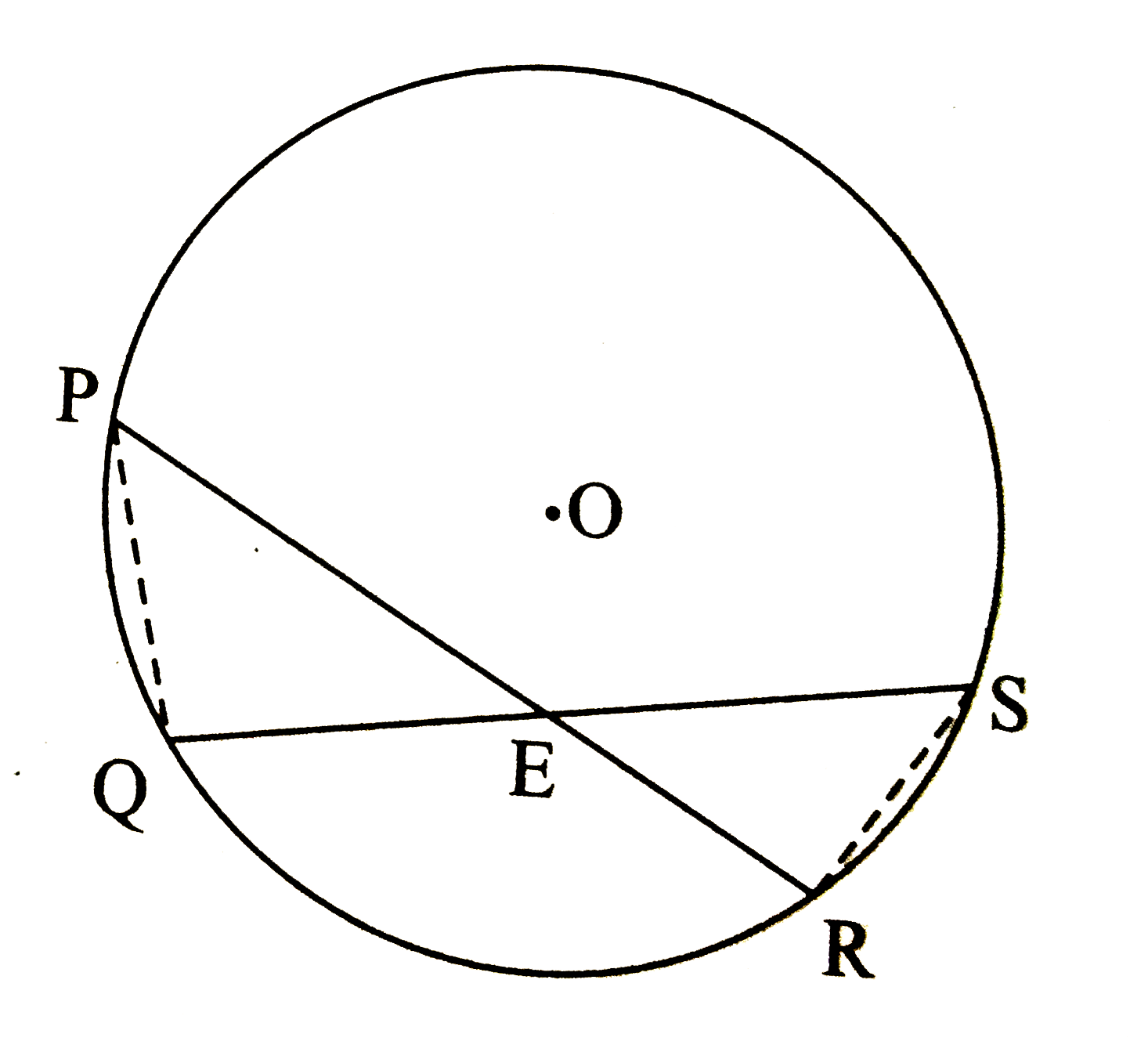
Given : (1) A circle with centre O .
(2) chords PR and QS intersect at point E inside the circle.
To prove : PE × ER = QE xx ES <br>Construction: Draw seg PQ and seg RS
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments ofone chord are equal to corresponding segments of the other chord.
View Solution
Knowledge Check
The length of a chord of a circle is equal to the radius of the circle. The angle which this chord subtends in the major segment of the circle is equal to :
A30∘B45∘C60∘D90∘The length of a chord of a circle is equal to the radius of the circle. The angle which this chord subtends in the major segment of the circle is equal to
A30∘B45∘C60∘D90∘Two chords AB and CD of a circle intersects each other at P. which of the following is correct?
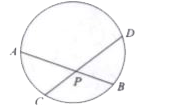 AAP×PB=CP×PDBAP+PB=CP×PDCAP−PB=CP−PDDAP×CP=BP×PD
AAP×PB=CP×PDBAP+PB=CP×PDCAP−PB=CP−PDDAP×CP=BP×PD
If the two equal chords of a circle intersect :
(i) inside
(ii) on
(iii) outside
the circle, then show that the line segment joining the point of intersection to the centre of the circle will bisect the angle between the chords.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the center makes equal angles with the chords.
View SolutionIf two equal chords of a circle in intersect within the circle, prove that : the segments of the chord are equal to the corresponding segments of the other chord. the line joining the point of intersection to the centre makes equal angles with the chords.
View SolutionIf two equal chords of a circle in intersect within the circle, prove that: the segments of the chord are equal to the corresponding segments of the other chord. the line joining the point of intersection to the centre makes equal angles with the chords.
View SolutionIf two chords of a congruent circle are equal; then their corresponding arcs are also equal.
View Solution
