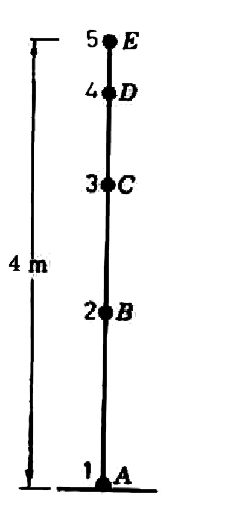
Drops of water trickles down from the ceiling at regular intervals of time such that the fourth drop will just drop freely after the first drop reaches the floor. Find the position of 2nd and 3rd drop from the floor. Assume that the ceiling is 8 m from the floor. Solution in Kannada
For a free fall,

a:b:c::1:3:5
∴a=19×8m=89=0.89m
b=39×8m=249=2.67m
c=59×8m=409=4.44m
From the figure distance of third drop from the ground =DB=c+b
=4.44+2.67
=7.11m.
Topper's Solved these Questions
- BOOK - SUBHASH PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - FIVE MARKS QUESTIONS WITH ANSWERS3videos
MOTION IN A STRAIGHT LINE
- BOOK - SUBHASH PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - NUMERICALS WITH SOLUTIONS11videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - SUBHASH PUBLICATIONCHAPTER - MOTION IN PLANEEXERCISE - NUMERICALS WITH SOLUTIONS47videos
MOTION IN PLANE
Similar Questions
Show that v=v0+at by graphical method.
06:00View SolutionCalculate the percentage increase in length of a wire of diameter 0.40 mm, stretched by a load of 5 kg. (Given: Young's modulus of elasticity of material of the wire 12.5×1010Nm−2)
06:09View SolutionTwo forces 8N and 5N are acting at a point on a body at an angle 120∘ then find the (i) magnitude and (ii) direction of their resultant.
03:20View SolutionWater drops fall from a tap on to the floor 5.0 m below at regular intervals of time. The first drop strikes the floor when the fifth drops beings to fall. The height at which the third drop will be from ground at the instant when the first drop strikes the ground is (take=g=10m−2)
05:44View SolutionDrops of water fall from the roof of a building 9m. High at regular intervals of time, the first drop reaching the ground at the same instant fourth drop starts to fall. What are the distance of the second and third drops from the roof?
06:19View SolutionWater drops from the nozzle of a shower into the stall floor 176.4 m below. The drops fall at regular interval of time, the first drop striking the floor at the instant the fourth drop begins to fall. Find the location of the individual drops when a drop strikes the floor. Take g = 9.8 m//s^(2)
04:15View Solutionwater drops trickle out from a nozzle and fall on the height 4.0 m below at regular intervals. When first drop reaches the floor, the fifth drop begins to fall. Find the positive of the drops , when a drop just strikes the floor.
 06:55View Solution
06:55View SolutionWater drops fall from a tap on the floor 5 m below at regular intervals of time, the first drop striking the floor when the fifth drop begins to fall. The height at which the third drop will be, from ground, at that instant when first drop strikes the ground, will be, (taking g = 10 ms^(-2))
View SolutionFrom an overhead tank water drops are falling at regular intervals of time of 17s .At the instant the first drop hits the ground,the 8th drop is about to leave the tank.At that instant,distance between 2nd and 3rd drops is
03:21View SolutionFrom an overhead tank water drops are falling at regular intervals of time of "1/7s" .At the instant the first drop hits the ground,the 8th drop is about to leave the tank.At that instant,distance between 2nd and 3rd drops is
06:55View SolutionWater drops are falling at regular intervals from the defective roof of a room of height 6 m. When the first drop touches this floor the third drop is about to fall from the roof. What would be the height above the floor of the second drop at that instant ?
View SolutionWater drops are falling at a regular interval from a leaked pipe 18m above the floor. When first drop touches the ground, fourth drop is just leaving the pipe. What is the height of third drop at the given instant?
View SolutionWater drips from the nozzle of a shower onto the floor 200 cm below. The drops fall at regular ( equal) intervals of time, the first drop striking the floor at the instant the fourth drop begins to fall. When the first drop strikes the floor, how far below the nozzle are the (a) second and (b) third drops ?
View SolutionIf water drops are falling at regular time intervals from ceiling of height H, then position of drop from the ceiling is (when n^(th) drop falling from the ceiling and r^(th) drop is in its way)
View SolutionWater drops fall from the roof of a building 20 m high at regular time intervals. If the first drop strikes the floor when the sixth drop begins to fall, the heights of the second and fourth drops from the ground at that instant are
View Solution

