Water drops from the nozzle of a shower into the stall floor 176.4 m below. The drops fall at regular interval of time, the first drop striking the floor at the instant the fourth drop begins to fall. Find the location of the individual drops when a drop strikes the floor. Take g=9.8m/s2
The correct Answer is:[78.4 m, 19.6 m]
Step by step video, text & image solution for Water drops from the nozzle of a shower into the stall floor 176.4 m below. The drops fall at regular interval of time, the first drop striking the floor at the instant the fourth drop begins to fall. Find the location of the individual drops when a drop strikes the floor. Take g = 9.8 m//s^(2) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Discussion Question18videos
KINEMATICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Conceptual MCQs Single Option Correct35videos
KINEMATICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Unsolved Numerical Pro.83videos
KINEMATICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Unsolved Numerical94videos
GRAVITATION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - exercise 1.33videos
LINEAR MOMENTUM & ITS CONSERVATION
Similar Questions
Water drips from the nozzle of a shower onto the floor 200 cm below. The drops fall at regular ( equal) intervals of time, the first drop striking the floor at the instant the fourth drop begins to fall. When the first drop strikes the floor, how far below the nozzle are the (a) second and (b) third drops ?
View SolutionWater drops are falling from a nozzle of a shower onto the floor, from a height of 9.8 m. The drops fall at a regular interval of time. When the first drop strikes the floor, at that instant, the third drop begins to fall. Locate the position of second drop from the floor when the first drop strikes the floor.
View Solution
Knowledge Check
- Question 1 - Select One
Water drops fall from a tap on to the floor 5.0 m below at regular intervals of time. The first drop strikes the floor when the fifth drops beings to fall. The height at which the third drop will be from ground at the instant when the first drop strikes the ground is (take=g=10m−2)
A1.25 mB2.15 mC2.75 mD3.75 m - Question 2 - Select One
Drops of water fall from the roof of a building 9m. High at regular intervals of time, the first drop reaching the ground at the same instant fourth drop starts to fall. What are the distance of the second and third drops from the roof?
A6 m and 2 mB6 m and 3 mC4 m and 1 mD4 m and 2 m - Question 3 - Select One
Water drops fall at regular intervals from a tap 5 m above the ground. The third drop is leaving the tap, the instant the first drop touches the ground. How far above the ground is the second drop at that instant. (g=10ms−2)
A1.25mB2.50mC3.75mD4.00m
water drops trickle out from a nozzle and fall on the height 4.0 m below at regular intervals. When first drop reaches the floor, the fifth drop begins to fall. Find the positive of the drops , when a drop just strikes the floor.
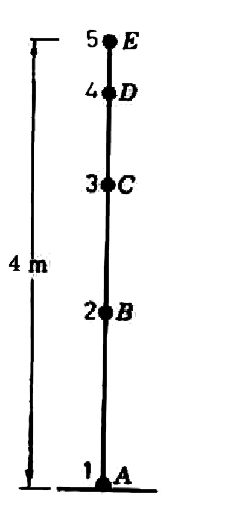 View Solution
View SolutionDrops of water from the roof of a house 6 m high fall at regular intervals. The first drop reaches the ground at an instant of time when third drop leaves the roof. Find the height of the second drop at that instant
View SolutionFrom the top of a building, 16 m high water drop are falling at eqal intervals of time such that when the first drop reaches the ground, the fifth drop just starts. Find the distance between the successive drops at hat instant.
View SolutionDrops of water fall at regular intervals from the roof of a building of height h=16m. The first drop striking the ground at the same moment as the fifth drop is ready to leave from the roof. Find the distance betweent he successive drops.
View SolutionWater drops fall at regular intervals from a roof. At an instant when a drop is about to leave the roof, the separations between 3 successive drops below the roof are in the ratio
View Solution

