Show that a=v2r and hence obtain an expression for centripetal force.Solution in Kannada
Let →r and →r, be the position vectors and →v velocities of the object when it is it point P and P. By definition, velocity at a point is along the tangent at that point in the direction of the motion. Since the path is circular, →v is perpendicular to →r and →v is perpendicular to →r
Therefore, △→v is perpendicular to △→r. Average acceleration △→v△t is perpendicular to △→r
The magnitude of →a is, by definition, given by |→a|=lim△t→0△→v△t
The triangle formed by the position vectors is similarly to the triangle formed by the velocity vectors.
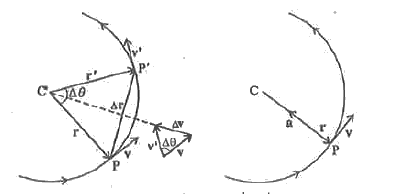
i.e, |△→v|v=|△→r|r or |△→v|=v(|△→r|)r
Therefore, |→a|=lim∣△→v△t=lim△t→0v|△→r|r△t=→vrlim△t→0|△→r|△t
If △t is very small, △θ will also small. The arc PP' is approximately equal to |△→r|
i.e., lim△t→0|△→r|△t=v Thus, centripetal acceleration |→a|=vfv=v2r and →a=vrd→rdt
The centripetal acceleration is always directed towards the centre. The centripetal force=ma.
Topper's Solved these Questions
- BOOK - SUBHASH PUBLICATIONCHAPTER - MOTION IN PLANEEXERCISE - NUMERICALS WITH SOLUTIONS47videos
MOTION IN PLANE
- BOOK - SUBHASH PUBLICATIONCHAPTER - MOTION IN PLANEEXERCISE - THREE MARKS QUESTIONS WITH ANSWERS7videos
MOTION IN PLANE
- BOOK - SUBHASH PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NUMERICALS WITH SOLUTIONS28videos
MOTION IN A STRAIGHT LINE
- BOOK - SUBHASH PUBLICATIONCHAPTER - OSCILLATIONSEXERCISE - NUMERICALS WITH SOLUTIONS41videos
OSCILLATIONS
Similar Questions
Two forces 8N and 5N are acting at a point on a body at an angle 120∘ then find the (i) magnitude and (ii) direction of their resultant.
03:00View SolutionDistinguish between resultant and equilibrant forces.
06:18View SolutionThe position coordinate of a moving particle is given by x=6+18t+9t2 ('x' in 'm' and 't' is 's') what is its velocity at t=2s?
05:46View SolutionCalculate total energy of a particle of mass 2.0×10−3kg oscillating simple harmonically with angular frequency 0.45 rad s−1 and amplitude 1.0×10−3m.
03:00View SolutionObtain an expression for the centripetal force F acting on a particle of mass m moving with velocity v in a circle of radius r . Take dimensionless constant K = 1 .
02:25View Solutionयदि अभिकेन्द्रीय बल F का मान कण के द्रव्यमान m, कण के वेग v तथा वृत्ताकार पथ की त्रिज्या r पर निर्भर करता है, तो विमीय विधि से अभिकेन्द्रीय बल का व्यंजक प्राप्त कीजिए।
03:09View SolutionCentripetal force (F) on a body of mass (m) moving with uniform speed (v) in a circle of radius (r ) depends upon m, v and r. The formula for the centripetal force using theory of dimensons.
03:03View SolutionObtain an expression for the centripetal force F acting on a particle of mass m moving with velocity v in a circle of radius r . Take dimensionless constant K = 1 .
View SolutionDimensionally prove the expression (mv^(2))/( r) for the centripetal force F acting on a particle of mass m moving with velocity v in a circle of radius r.
03:18View SolutionA particle of mass m is moving in a circular path of radius r with a uniform speed v. The centripetal force on the body is (m omega^(2))/( r) . When the particle is displace half of the distance, then what is the work done by the centripetal force?
12:24View SolutionFor object moving on circular path centripetal force (F) depend on mass (m), velocity (v) and radius (r). Derive equation of centripetal force F.
03:49View SolutionThe centripetal force on a body of mass 'm' and velocity 'v' moving in circular orbit of radius 'r' is given by F = mv2r. Using the formula of centripetal force write an quation to find percentage error in centripetal force.
01:25View SolutionDefine centripetal force. Derive an expression for it.
02:13View SolutionWhat is centripetal force? Derive an expression for it. Show that centripetal force does no work.
01:38View SolutionObtain an expression for the centripetal force required to make a body of mass m moving with a constant speed v around a circular path of radius r.
01:51View Solution

