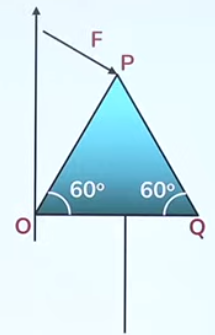
Find the torque about the point 'A' in the following diagram
Text Solution

(1) Torque due to 20N : about A=O
(2) Torque due to 10N=10×0.8=8N (C wise)
Torque due to 25N =(25sin25∘) (AC wise)
=25×0.8sin25∘
=25×0.8×0.4225=845nm
Net torque =0−8N(CW)+8.45(ACW)
=0.45 anticlockwise
|
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - SUBHASH PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - FIVE MARKS QUESTIIONS WITH ANSWERS
6 Videos
- SUPER MODEL QUESTION PAPER 2BOOK - SUBHASH PUBLICATIONCHAPTER - SUPER MODEL QUESTION PAPER 2EXERCISE - QUESTION PAPER -2 (FOR PRACTICE) (PART-D)
10 Videos
- THERMAL PROPERTIES OF MATTERBOOK - SUBHASH PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - FOUR MARKS QUESTIONS AND ANSWERS
22 Videos
Similar Questions
Knowledge Check
Find the torque about the origin when a force of 3ˆj N acts on a particle whose position vector is 2ˆk m
A5ˆjNmB−6ˆiNmC6ˆkNmD6ˆiNmChoose the correct statement about the following diagram
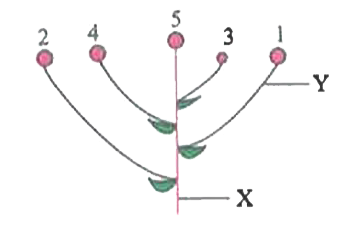 AX in the diagram represents branched peduncleBFlowers are arranged in centrifugal mannerCY in the diagram represents pedicel of the flowerDIt is a simple umbel inflorescence
AX in the diagram represents branched peduncleBFlowers are arranged in centrifugal mannerCY in the diagram represents pedicel of the flowerDIt is a simple umbel inflorescenceThe torque →τ on a body about a given point is found to be equal to →A×→L where →A is a constant vector and →L is the angular momentum of the body about the point. From this its follows that -
Ad→Ldt is perpendicular to →L at all instants of time.Bthe components of →L in the direction of →A does not change with time.Cthe magnitude of →L does not change with timeD→L does not change with time.
Calculate the resultant torque from the following diagram:

View SolutionFind the total torque acting on the body shown in the figure about the point O.
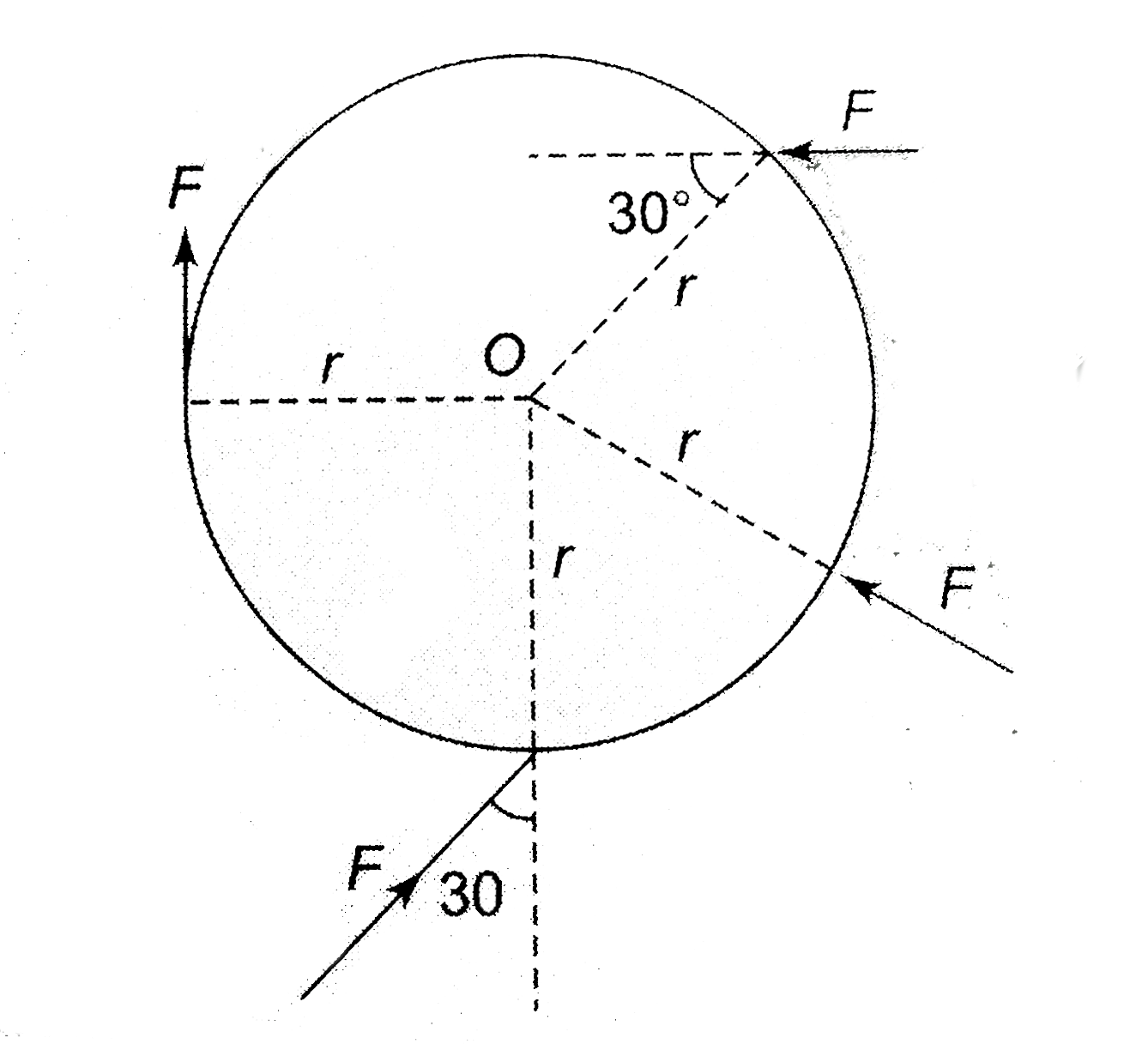
View SolutionFind the torque of forces about O
(a)
(b)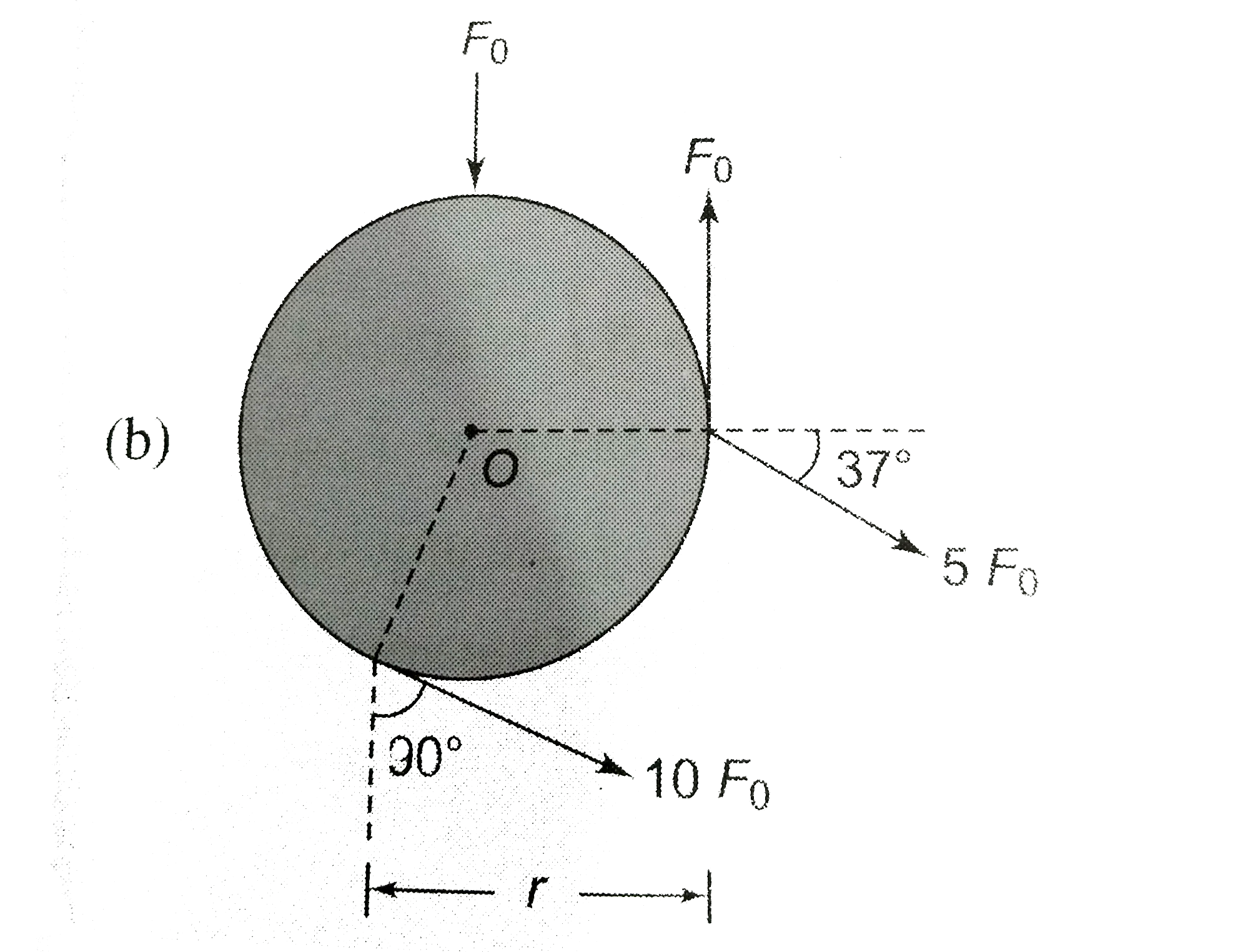
View SolutionThe torque τ on a body about a given point is found to be equal to AxxL where A is a constant vector, and L is the angular momentum of the body about that point. From this it follows that
View SolutionA particle describes uniform circular motion. Find the torque on it about the centre of the circle.
View Solution