Four point charges – q, + q, + q and – q are placed on y-axis at y = – 2d, y = – d, y = + d and y = + 2d, respectively. The magnitude of the electric field E at a point on the x-axis at x = D, with D >> d, will behave as:
E∝1D4
E∝1D
E∝1D2
E∝1D3
The correct Answer is:A
Electric field at p=2E1cosθ1−2E1cosθ2
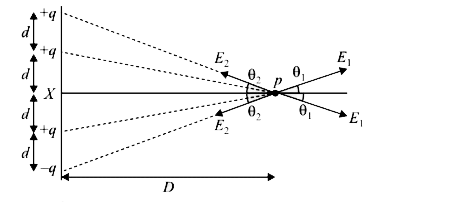
=3kq(d2+D2)×D(d2+D2)1/2−2kq[(2d)2+D2]×D[(2d)2+D2]1/2
=2kqD[(d2+D2)−3/2−(4d2+d2)−3/2]
=2KqDD3[(a+d2D2)−3/3−(1+4d2D2)−3/2]
Applying binominal approximation ∴d<<D
=2KqDD3[1−32d2D2−(1−3×4d22D2)]
=2KqDD3[122d2D2−32d2D2]
=9Kqd2D4
Similar Questions
चार बिंदु आवेशों −q,+q,+q और −q को Y-अक्ष पर क्रमशः y=−2d,y=−d,y=+d तथा y=+2d पर रखा गया है। X-अक्ष पर उपस्थित एक बिंदु x=D जहाँ D>>d है,पर विद्युत क्षेत्र के परिमाण का व्यवहार होगा
11:36View Solutionचार बिन्दु आवेशों −q,+q,+q और −q को y- अक्ष पर, क्रमशः y=−2d,y=−d,y=+d तथा y=+2d पर रखा गया है | x - अक्ष पर उपस्थित एक बिन्दु x = D, जहाँ, D>>d है, पर विद्युत क्षेत्र के परिमाण E का व्यवहार होगा
06:41View Solutionचार बिन्दु आवेशों -q, + q, + q और -q को Y.अक्ष पर क्रमश: y= -2d, y= -d, y= + d तथा y = + 2d पर रखा गया है। X-अक्ष पर उपस्थित एक बिन्दु x = D, जहाँ D>>d है, पर विद्युत क्षेत्र के परिमाण E का व्यवहार होगा
12:40View Solutionदो बिन्दु आवेश +q तथा −q(x,y) समतल के दो बिंदुओं क्रमशः (−d,0) तथा (d,0) पर रखे है, तब
04:00View SolutionIn ΔABC and ΔPQR, AB=PQ, BC=QR and CB and RQ are extended to X and Y respectively and ∠ABX=∠PQY. Prove that ABC≅ PQR.
03:13View SolutionFour points charges -q,+q,+q and -q are placed on y-axis at y=-2d, y=-d,y=+d and y=+2d, respectively. The magnitude of the electric field E at a point on the x-axis at x=D, with D>>d, will behave as :
07:03View SolutionIf xpyq = (x+y)^(p+q),then(d^2y)/(dx2) =..........
06:26View SolutionTwo point charges (Q each are placed at (0,y) and (0-y) A point charge q of the same polarity can move along the x-axis. Then
05:32View Solution

