The given plots represent the variation of the concentration of a reactant R with time for different reactions (i) and (ii). The sum of orders of the reactions is ________ .
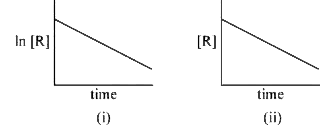
The correct Answer is:1
axa−xx
For 1st order reaction
+dxdt=k(a−x)1
∫dxa−x=∫kdt
−ln(a−x)=kt+c
If t=0
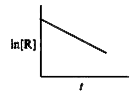
If t=0
c=−lna∴−ln(a−x)=kt−lna or ln(a−x)=−kt+lna v m x C
Similarly
R(A0)(A)→P
−d[R](A)dt=k[R]0
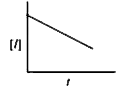
or −d(R)=kdt or ∫d[R]=−∫kdt
[R]=−kt+c or [A]=−kt+cy=mx+c
Similar Questions
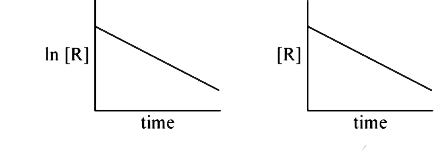
The given plots represent the variation of the concentration of a reactant R with time for different reactions (i) and (ii). The respective orders of the reactions are:
 View Solution
View SolutionThe given plots represent the variation of the concentration of a reactant R with time for two different reaction (i) and (ii) The respective orders of the reactions are
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The given plots represent the variation of the concentration of a reactant R with time for two different reaction (i) and (ii) The respective orders of the reactions are
 A1,0B1,1C0,1D0,2
A1,0B1,1C0,1D0,2 - Question 2 - Select One
For a first order reaction, the concentration of reactant :
Ais independent of timeBvaries linearly with timeCvaries exponentially with timeDNone - Question 3 - Select One
If initial concentration is doubled, the time for half-reaction is also doubled, the order of reaction is
AZeroBOneCTwoDThree
A reaction on increasing the concentration of reactant by 8 times the rate of reaction gets doubled. The order of reaction
View SolutionIn a reaction if the concentration of reactant A is tripled, the rate of reaction becomes twenty seven times. What is the order of reaction?
View SolutionIn a reaction if the concentration of reactant A is tripled, the rate of reaction becomes twenty seven times. What is the order of reaction?
View SolutionFor a second order reaction, half-life concentration of reactants:
View SolutionFor a given reaction the logarithm of the concentration of the reactant plotted against time gave a straight line with negative slope . The order of the reaction is
View Solution

