Two particles of masses M and 2M, moving as shown, with speeds of 10 m/s and 5 m/s, collide elastically at the origin. After the collision, they move along the indicated diretions with speeds $v_{1}$ and $v_{2}$ respectively. The value of $v_{1}$ and $v_{2}$ are nearly:

A

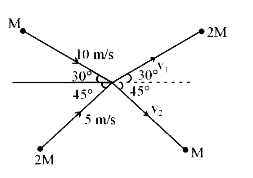
6.5 m/s and 6.3 m/s

B

3.2 m/s and 6.3 m/s

C

3.2 m/s and 12.6 m/s

D

6.5 m/s and 3.2 m/s

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

From conservation of momentum
Along x-direction.
$M (10) {cos 30}^{\circ} + (2 M) (5) {cos 45}^{\circ} = (2 M) . v_{1} {cos 30}^{\circ} + M . v_{2} {cos 45}^{\circ}$
$\Rightarrow \sqrt{3} v_{1} + \frac{v_{2}}{\sqrt{2}} = 5 \sqrt{3} + 5 \sqrt{2}$ ………..(1)
Along y-direction.
$(2 M) \times (5) {sin 45}^{\circ} - M (10) {sin 30}^{\circ} = (2 M) v_{1} {sin 30}^{\circ} - M y_{2} {sin 45}^{\circ} \Rightarrow v_{1} - \frac{v_{2}}{\sqrt{2}} = 5 \sqrt{2} - 5$ ............(2)
Solving (1) and (2)
$v_{1} = 6.5 m / s$ , $v_{2} = 6.3 m / s$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Similar Questions

Knowledge Check

Question 1 - Select One
Two particles of mass m and 2 m moving in opposite directions collide elastically with velocities v and 2v. Find their velocities after collision.
A0, 3v
B1, 3v
C0, 1v
D0, 4v
Question 2 - Select One
Two equal masses $m_{1}$ and $m_{2}$ moving along the same straight line with velocites $+ 3 m / s$ and $- 5 m / s$ respectively collide elastically. Their velocities after the collision will be respectively.
A $+ 4 m / s$ for both
B $- 3 m / s and + 5 m / s$
C $- 4 m / s and + 4 m / s$
D $- 5 m / s and + 3 m / s$
Question 3 - Select One
A particle of mass m moving with speed V collides eleastically with another particle of mass 2mFind speed of smaller mass after head on collision
A $\frac{v}{3}$
B $- \frac{v}{3}$
C $\frac{2 v}{3}$
D $\frac{- 2 v}{3}$

Recommended Questions

Home
Ask Doubt
Profile