A circular disc of radius b has a hole of radius a at its centre (see figure). If the mass per unit area of the disc varies as (σ0r). then the radius of gyration of the disc about its axis passing through the centre is:
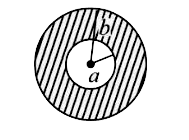
a+b2
√a2+b2+ab2
√a2+b2+ab3
a+b3
The correct Answer is:C
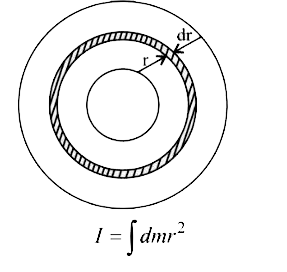
l=∫dmr2
⇒ ∫da(σ0r2πrdr)r2 ⇒ l=2σ0πb3(−a3)3 ⇒ l=mk2
⇒ 2σ0π(b3−a3)3=2σ0π(b−a)K2 ⇒ k=√a2+b2+ab3
Similar Questions
Knowledge Check
- Question 1 - Select One
Radius of gyration of a uniform circular disc about an axis passing through its centre of gravity and perpendicular to its plane is
AR/√2BR/2C√2 RD2R - Question 2 - Select One
The radius of of disc is 2 m the radius of gyration of disc about an axis passing through its diameter is
A2 mB2 cmC1 mD0.2 m - Question 3 - Select One
The radius of gyration of a disc about an axis coinciding with a tangent in its plane is
AR2BR√2C√2RD√52R
A uniform disc (of mass M and radius a) has a hole (of radius b) drilled through it. The centre of the hole is at a distance c from the centre of the original disc. What is the moment of inertia of the disc about an axis through the centre of the disc and perpendicular to its plane ?
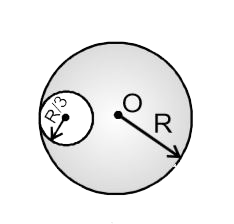
View SolutionA uniform disc of radius R has a round disc of radius R/3 cut as shown in Fig. The mass of the remaining (shaded) portion of the disc equals M. Find the moment of inertia of such a disc relative to the axis passing through geometrical centre of original disc and perpendicular to the plane of the disc.
 View Solution
View SolutionFrom a disc of radius R and mass m, a circular hole of diamter R, whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis, passing through the centre?
View SolutionFrom a disc of radius R and mass M, a circular hole of diameter R, whose rim passes through the centre is cut. What is the moment of inertia of remaining part of the disc about a perependicular axis, passing through the centre ?
View SolutionFrom a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed as shown in figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is
 View Solution
View Solution

