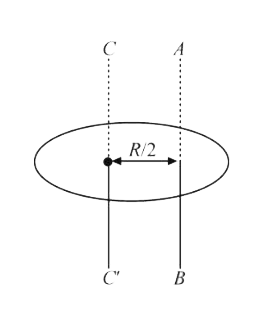
The radius of gyration of a uniform disc of radius R, about an axis passing through a point $\frac{R}{2}$ away from the centre of disc, and perpendicular to the plane of disc is:

A

$\sqrt{\frac{1}{2}} R$

B

$\sqrt{2} R$

C

$\frac{\sqrt{3}}{2} R$

D

$(\frac{\sqrt{3}}{4}) R$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$I_{A B} = I_{C C'} + m {(\frac{R}{2})}^{2}$
$I_{A B} = \frac{1}{2} m R^{2} + \frac{m R^{2}}{4}$ , $I_{A B} = \frac{3 m R^{2}}{4}$
$m k^{2} = \frac{3 m R^{2}}{4}$ , $k = \sqrt{\frac{3 R^{2}}{4}}$
$k = \frac{\sqrt{3} R}{2}$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Similar Questions

Knowledge Check

Question 1 - Select One
The radius of gyration of a uniform solid sphere of radius R., about an axis passing through a point $\frac{R}{2}$ away from the centre of the sphere is:
A $\sqrt{\frac{13}{20}} R$
B $\sqrt{\frac{23}{40}} R$
C $\sqrt{\frac{23}{20}} R$
D $\sqrt{\frac{13}{40}} R$
Question 2 - Select One
The radius of gyration of a uniform circular disc of radius $R$ , about any diameter of the disc is
A $K = R$
B $K = R / 2$
C $K = 2 R$
Dnone of these
Question 3 - Select One
The radius of gyration of a disc of mass 100 g and radius 5 cm about an axis passing through its centre of gravity and perpendicular to the plane is
A0.5 cm
B2.5 cm
C3.54 cm
D6.54 cm

Recommended Questions

Home
Ask Doubt
Profile