The stopping potential (in volt) as a function of frequency (v) for a sodium emitter, is shown in the figure. The work function of sodium, from the data plotted in the figure, will be:
(Given : Planck’s constant)
)
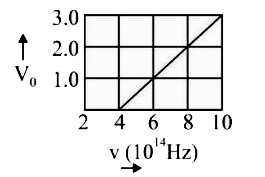
1.95 eV
2.12 eV
1.66 eV
1.82
The correct Answer is:C
Similar Questions
Knowledge Check
The work function of a photoelectric material is 3.3 V. the threshold frequency will be equal to [Given that h=6.6×10−34Js]
A8.0×1014HzB8.0×1034HzC5.0×1015HzD5.0×1019HzThe wavelength of th first spectral line of sodium 5896 Å . The fisrt excitation potential of sodium atomm will be (Planck's constant h=6.63×10−34J−s)
A4.2VB3.5VC2.1VDNone of theseCalculate the energy in joule corresponding to light of wavelength 45nm :
(Planck' constant h=6.63×10−34Js , speed of light c=3×108ms−1)A6.67×1012B4.42×10−13C4.42×10−18D6.67×1012
If the work function of a and is 3 eV, calculate the threshold wavelength of that metal.
(Velocity of light =3×108m/s Planck's constant= 6.63×10−34J−s,1eV=1.6×10−19)
View SolutionCalculate the wavelength of light incident on a material of work function 2.0 eV if the stopping potential is 1.0 V .
Given h=6.625×10−34 Js and mass of electron =9.1×10−31kg
View SolutionCalculate the energy in joule corresponding to light of wavelength 45 nm (Planck.s constant h=6.63×10−34 Js, speed of light c=3×108ms−1)
View SolutionA student performs an experiment on photoelectric effect using two materials A and B. A plot of stopping potential (V0) vs frequency (ν) is as shown in the figure.
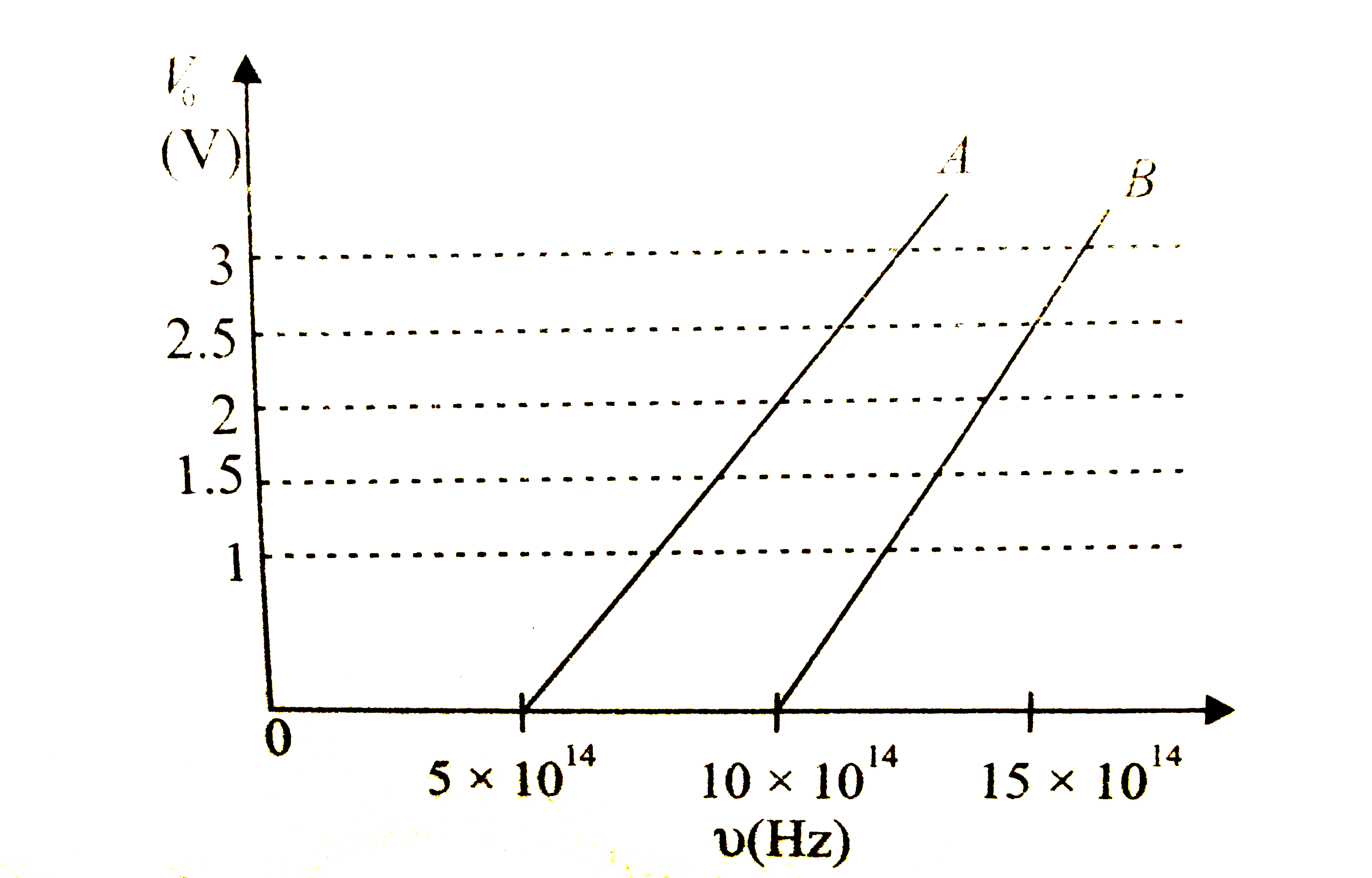
The value of Planck's constant obtained from the experiment for both A and B respectively is
(Given electric charge of an electron =1.6×10−19C)
View SolutionThe value of Planck's constant is 6.62618×10−34Js. The number of significant figures in it is
View Solution
