O' is the centre of the inscribed circle in a 30∘−60∘−90∘ΔABC with right angled at C. If the circle is tangent to AB at D then the angle ∠COD is
Step by step video & image solution for O' is the centre of the inscribed circle in a 30^@ - 60^@ -90^@ DeltaABC with right angled at C. If the circle is tangent to AB at D then the angle /_COD is by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Let ‘O’ be the centre of a circle, PQ is a diameter, then prove that ∠PRQ=90∘ (OR) Prove that angle in a semi-circle is right angle.
View SolutionLet ‘O’ be the centre of a circle, PQ is a diameter, then prove that ∠PRQ=90∘ (OR) Prove that angle in a semi-circle is right angle.
View SolutionIf a chord AB subtends and angle of 60∘ at the centre of a circle, then the angle between the tangents to the circle drawn from A and B is
View SolutionPQ is tangent at a point R of the circle with centre O. If ST is a diameter of the circle and ∠TRQ=30∘ find ∠PRS
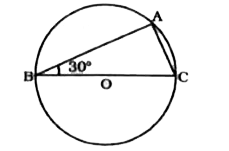
View SolutionAB is the diameter and AC is a chord of a circle with centre O such that angle BAC=30∘. The tangent to the circle at C intersects AB produced in D. Show that BC=BD.
View SolutionIf a circle is inscribed in right angled triangle ABC with right angle at B, show that the diameter of the circle is equal to AB+BC−AC.
View SolutionO' is the centre of the inscribed circle in a 30∘−60∘−90∘ΔABC with right angled at C. If the circle is tangent to AB at D then the angle ∠COD is
View SolutionIn the figure ΔABCis inscribed in a circle with centre O. If ∠ABC=30∘ then ∠ACBis equal to
View Solution
