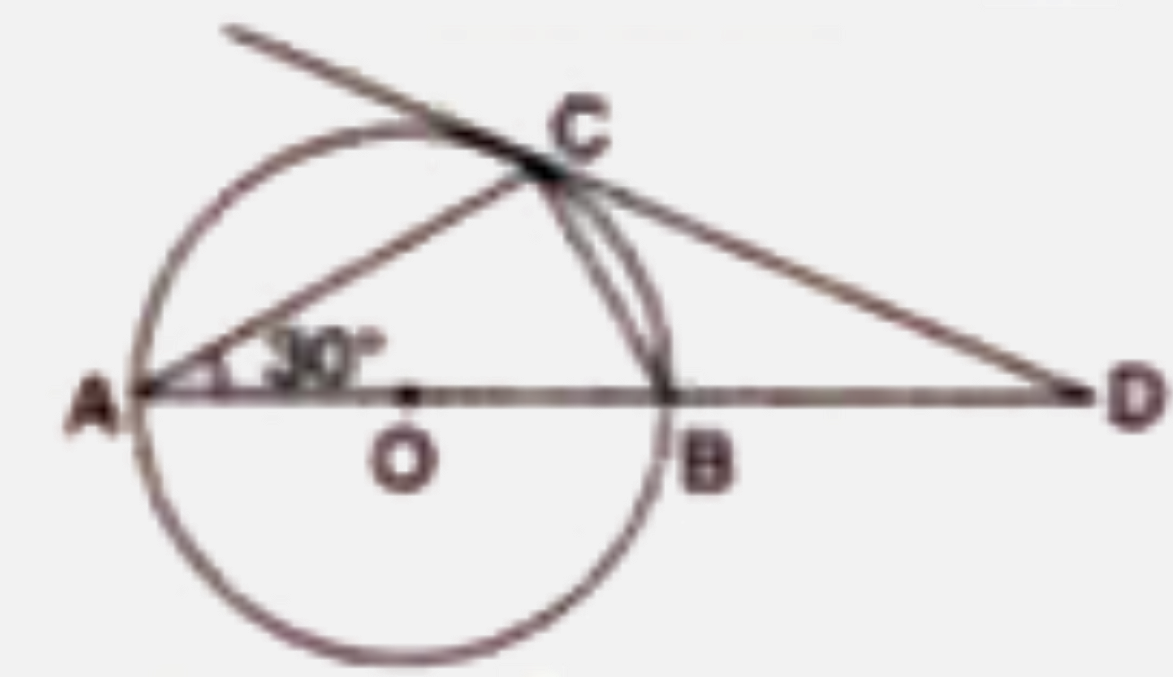
AB is the diameter and AC is a chord of a circle with centre O such that angle BAC=30∘. The tangent to the circle at C intersects AB produced in D. Show that BC=BD.
To solve the problem, we need to prove that BC=BD given that AB is the diameter of the circle, AC is a chord, and ∠BAC=30∘. The tangent at point C intersects the extended line of AB at point D.
1. Draw the Circle and Points:
- Draw a circle with center O.
- Mark points A and B on the circle such that AB is the diameter.
- Mark point C on the circle such that AC is a chord.
- Draw the tangent at point C which intersects the extended line AB at point D.
2. Identify Angles:
- Given ∠BAC=30∘.
- Since AB is the diameter, ∠ACB is a right angle (by the inscribed angle theorem).
3. Calculate Angle BOC:
- The angle at the center O corresponding to the arc AC is twice the angle at the circumference ∠BAC.
- Thus, ∠BOC=2×∠BAC=2×30∘=60∘.
4. Determine Angles in Triangle OCD:
- Since OC is the radius and CD is the tangent at point C, OC⊥CD. Therefore, ∠OCD=90∘.
- In triangle OCD, we have ∠BOC=60∘ and ∠OCD=90∘.
- The remaining angle ∠ODC can be calculated as:
∠ODC=180∘−∠BOC−∠OCD=180∘−60∘−90∘=30∘.
5. Angles in Triangle BCD:
- In triangle BCD, we know:
- ∠BDC=∠ODC=30∘ (from the previous step).
- ∠BCD=∠ACB=90∘.
- Therefore, the third angle ∠BCD can be calculated as:
∠BCD=180∘−∠BDC−∠BOC=180∘−30∘−90∘=60∘.
6. Using the Angles to Prove BC=BD:
- In triangle BCD, we have:
- ∠BDC=30∘
- ∠BCD=60∘
- ∠DBC=90∘
- Since ∠BDC=∠BCD, by the property of triangles, the sides opposite to equal angles are equal, thus:
BC=BD.
Conclusion:
We have shown that BC=BD.
- Draw a circle with center O.
- Mark points A and B on the circle such that AB is the diameter.
- Mark point C on the circle such that AC is a chord.
- Draw the tangent at point C which intersects the extended line AB at point D.
- Given ∠BAC=30∘.
- Since AB is the diameter, ∠ACB is a right angle (by the inscribed angle theorem).
- The angle at the center O corresponding to the arc AC is twice the angle at the circumference ∠BAC.
- Thus, ∠BOC=2×∠BAC=2×30∘=60∘.
- Since OC is the radius and CD is the tangent at point C, OC⊥CD. Therefore, ∠OCD=90∘.
- In triangle OCD, we have ∠BOC=60∘ and ∠OCD=90∘.
- The remaining angle ∠ODC can be calculated as:
∠ODC=180∘−∠BOC−∠OCD=180∘−60∘−90∘=30∘.
- In triangle BCD, we know:
- ∠BDC=∠ODC=30∘ (from the previous step).
- ∠BCD=∠ACB=90∘.
- Therefore, the third angle ∠BCD can be calculated as:
∠BCD=180∘−∠BDC−∠BOC=180∘−30∘−90∘=60∘.
- In triangle BCD, we have:
- ∠BDC=30∘
- ∠BCD=60∘
- ∠DBC=90∘
- Since ∠BDC=∠BCD, by the property of triangles, the sides opposite to equal angles are equal, thus:
BC=BD.
We have shown that BC=BD.
Topper's Solved these Questions
- TANGENTS AND INTERSECTING CHORDSBOOK - ICSECHAPTER - TANGENTS AND INTERSECTING CHORDSEXERCISE - EXERCISE 18 (C)
42 Videos
- TANGENTS AND INTERSECTING CHORDSBOOK - ICSECHAPTER - TANGENTS AND INTERSECTING CHORDSEXERCISE - EXERCISE 18(A)
24 Videos
- SPECIMEN QUESTION PAPER (MATHEMATICS)BOOK - ICSECHAPTER - SPECIMEN QUESTION PAPER (MATHEMATICS)EXERCISE - Section C
12 Videos
- TRIGONOMETRICAL IDENTITIESBOOK - ICSECHAPTER - TRIGONOMETRICAL IDENTITIESEXERCISE - QUESTIONS
22 Videos
Similar Questions
In the given figure AB is the diameter and AC is the chord of a circle such that ∠BAC=30∘. The tangent at C intersects AB produced at D. Prove that :BC=BD.
View SolutionAB is a diameter of a circle and AC is its chord such that ∠BAC=30∘. If the tengent at C intersects AB extended at D, then BC=BD.
View SolutionAB is a diameter of a circle and AC is its chord such that ∠BAC=30∘. If the tengent at C intersects AB extended at D, then BC=BD.
View SolutionIn Figure 2, AB and AC are tangents to the circle with centre O such that angle BAC = 40°. Then angle BOC is equal to
View SolutionIn figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then ∠BAT is equal to
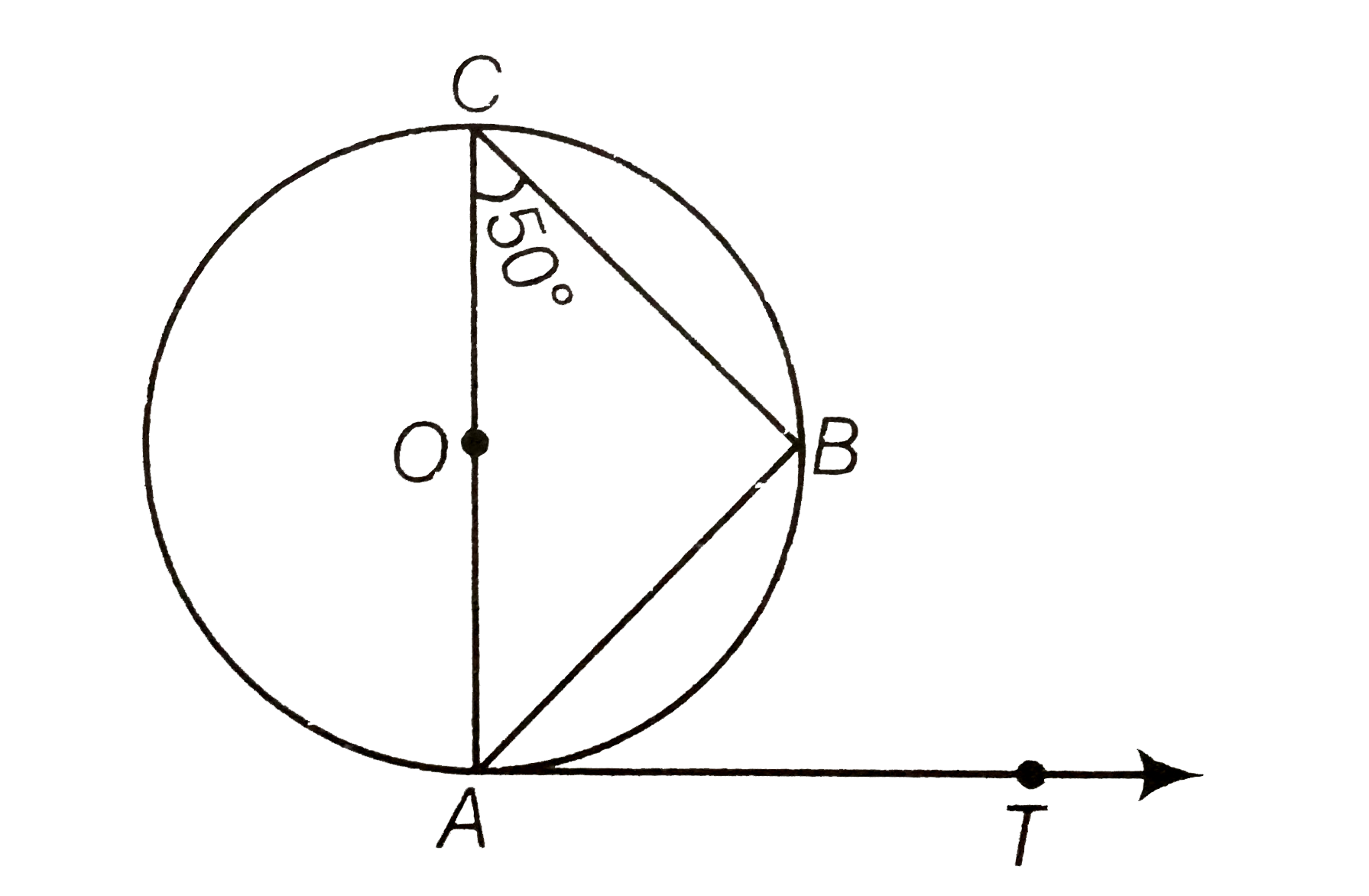
View SolutionIn figure, AB is a chord of the circle and AOC is the diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then angleBAT is equal to : (a) 45∘ , (b) 60∘ , (c) 50∘ , (d) 55∘
View SolutionIn the given figure, AB and XY are diameters of a circle with centre O. If ∠APX=30∘, find:
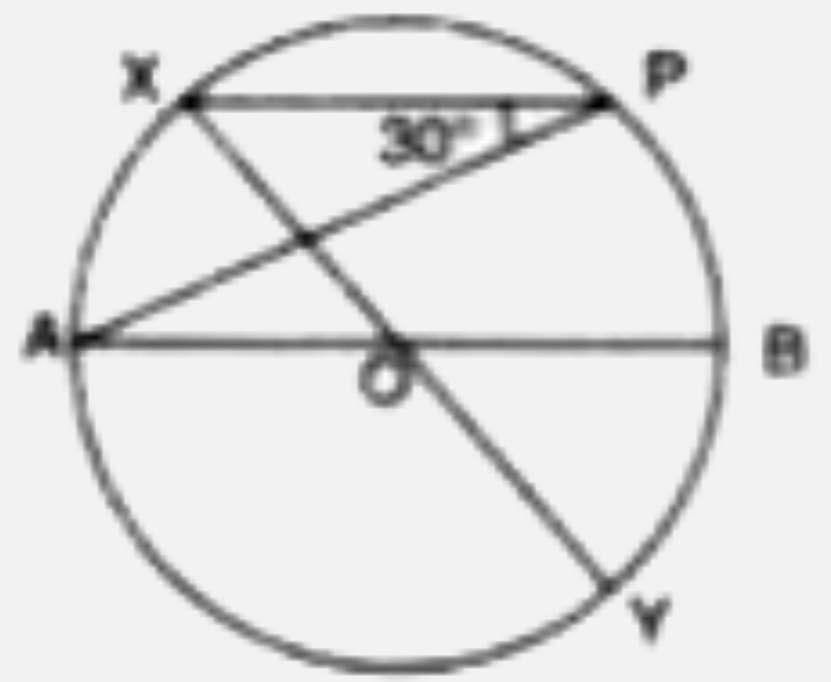
∠AOX
View SolutionIn the given figure, AB and XY are diameters of a circle with centre O. If ∠APX=30∘, find:

∠APY
View SolutionIn the given figure, AB and XY are diameters of a circle with centre O. If ∠APX=30∘, find:
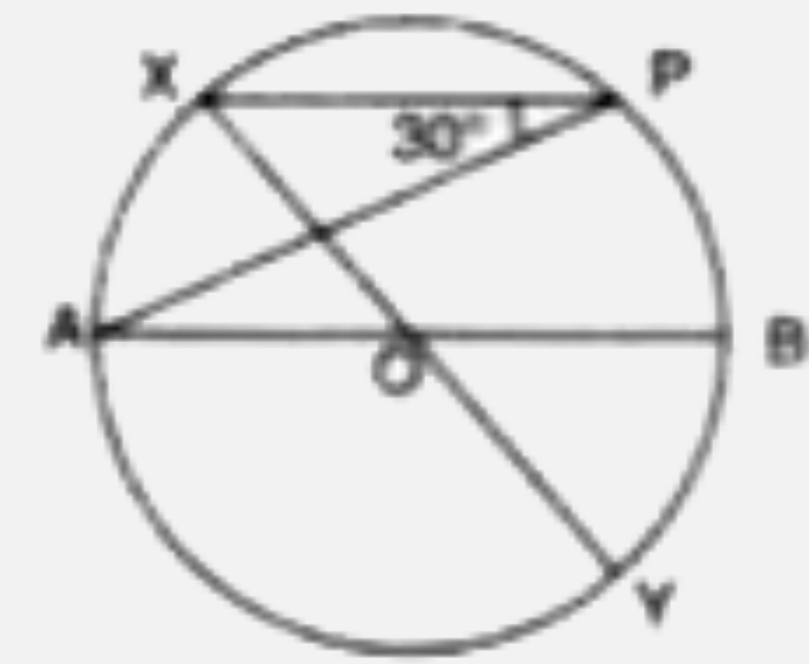
∠BPY
View SolutionIn the given figure, AB and XY are diameters of a circle with centre O. If ∠APX=30∘, find:

∠OAX
View Solution