64 globules of mercury each of radius. r and carrying q coalesce to form a big globule.Find the ratio between surface charge density of the big globule σ1 and surface charge density of the small globule σ2. σ1σ2 ?
Step by step video & image solution for 64 globules of mercury each of radius. r and carrying q coalesce to form a big globule.Find the ratio between surface charge density of the big globule sigma_(1) and surface charge density of the small globule sigma_(2). (sigma_(1))/(sigma_(2)) ? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
64 small drops of mercury each of radius r and charge q coalesce to form a big drop. The ratio of the surface density of charge of each small drop withh that of big drop is
A1:4B4:1C1:64D64:1 - Question 2 - Select One
A sphere has surface charge density σ. It is surrounded by a spherical shell. The surface charge density on the spherical shell is
AσB−σCzeroDσ2 - Question 3 - Select One
Surface charge density of soap bubble of radius r and surface tension T is σ.If P is excess pressure the value of σ is
Aε0[4Tr−P]32B[2ε0(4Tr−P)]12C4TrD[4ε0(2Tr−P)]12
Find the electric force experienced by a charge reduced to a unit area of an arbitary conductor if the surface density of the charge equals σ.
View SolutionThe electric intensity at a point near a charged conductor of surface charge density σ is
View SolutionTwo spherical conductors of radii 4 m and 5 m are charged to the same potential. If σ1andσ2 be the respective value of the surface density of charge on the two conductors, then the ratio σ1σ2is
View SolutionFor the hemisphere of radius R shown in the figure the surface charge density σ varies with θ (shown in figure) as σ=σ0cosθ the total charge on the sphere is
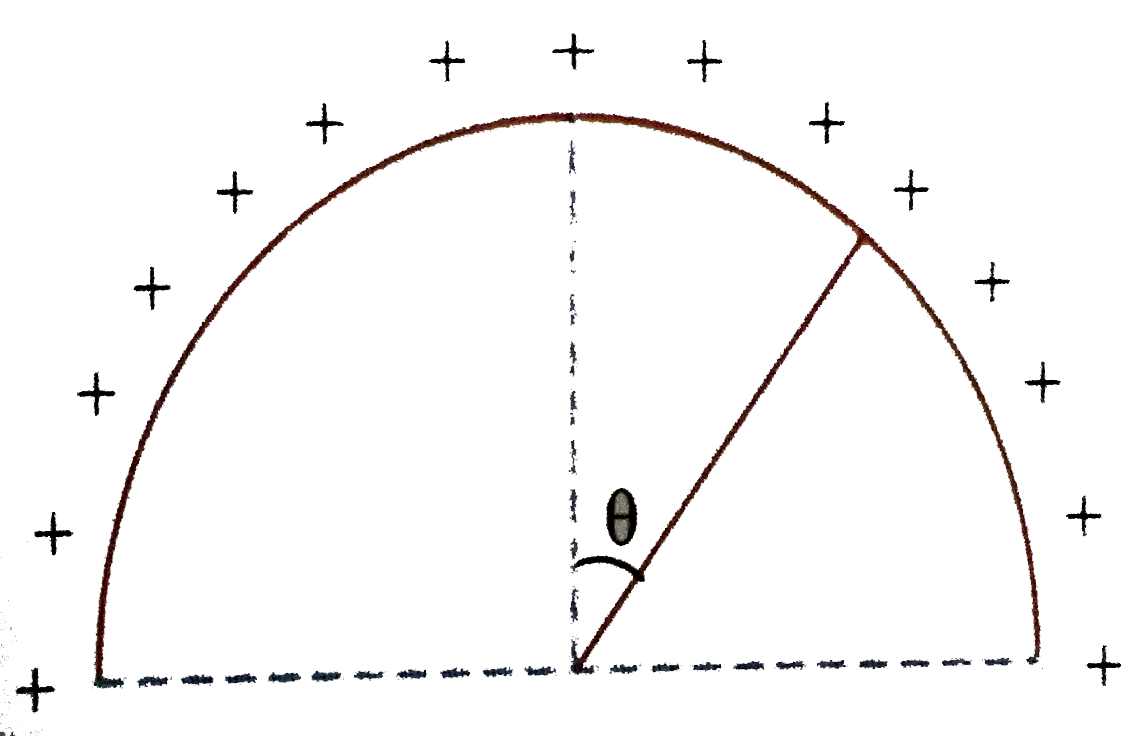 View Solution
View SolutionWhen a charge of amount Q is given to an isolated metal plate X of surface area A, its surface charge density becomes σ1. When an isolated identical plate Y is brought close to X the surface charge density on X becomes σ2. When Y is earthed the surface charge density on X becomes σ3. Choose the incorrect option.
View Solution
