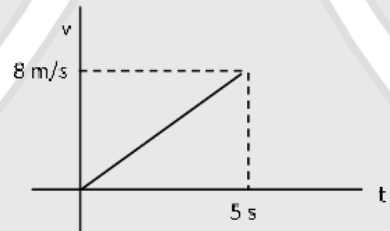
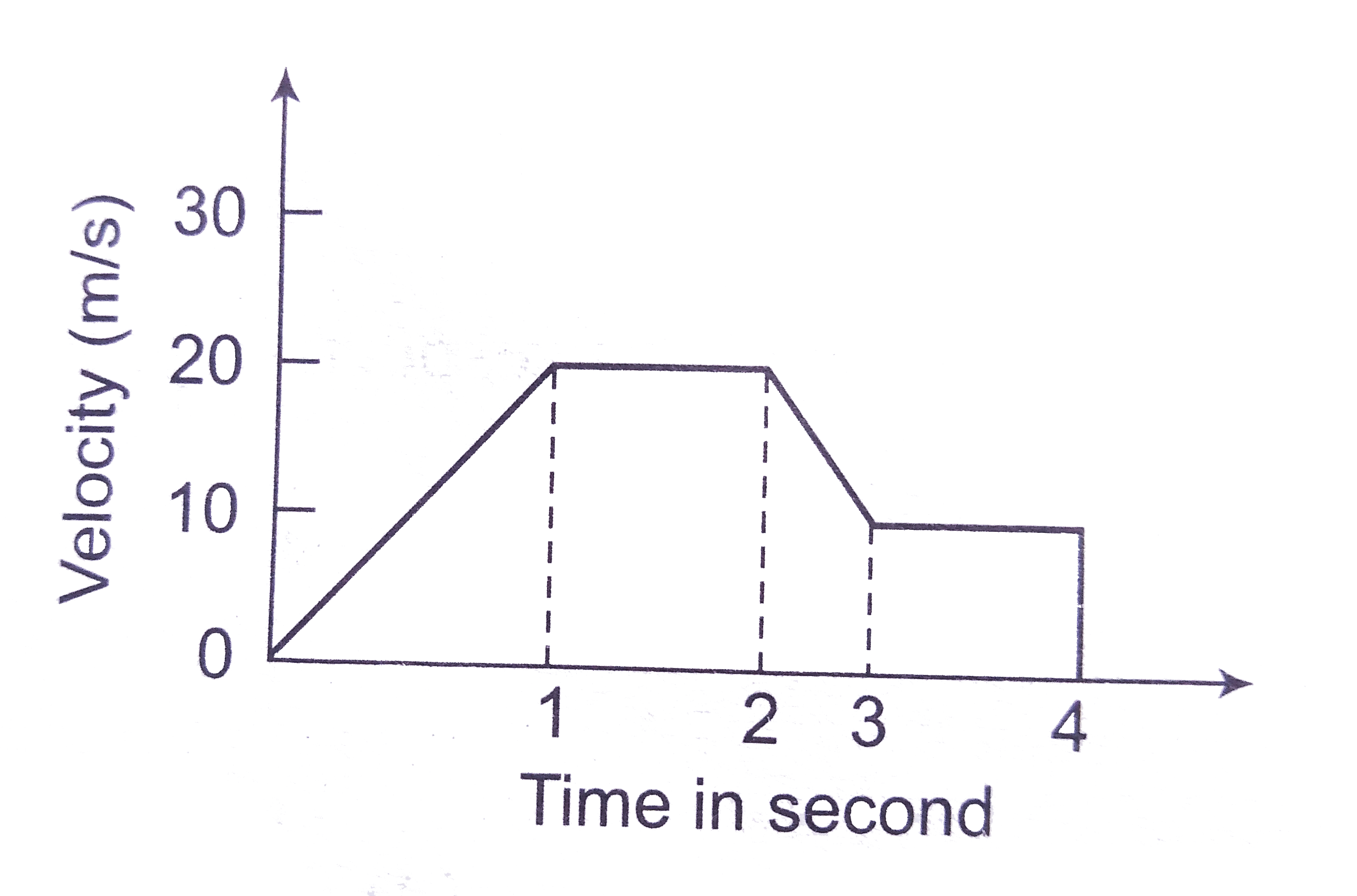
The v−t graph for a particle is shown. The distance travelled in the first four seconds is:
12 m
16 m
20 m
24 m
The correct Answer is:B
Area below v−t curve provides displacement
Hence, s=∫u0dt
Topper's Solved these Questions
- BOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - More than one choice is correct16videos
MOTION IN A STRAIGHT LINE
- BOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Assertion Reason12videos
MOTION IN A STRAIGHT LINE
- BOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Problems and Practice16videos
MOTION IN A STRAIGHT LINE
- BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type11videos
FRICTION AND CIRCULAR MOTION
- BOOK - GRB PUBLICATIONCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - All Questions210videos
MOTION IN TWO AND THREE DIMENSIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
The v-t graph for a particle is as shown. The distance travelled in the first seconds is :
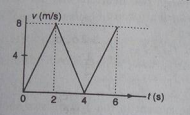A12 mB16 mC20 mD24 m - Question 2 - Select One
The v-t graph for a particle is as shown. The distance travelled in the first seconds is :
A12 mB16 mC20 mD24 m - Question 3 - Select One
Figure shows the speed versus time graph for a particle. Find the distance travelled by the particle during the time t=0 to t=3s.
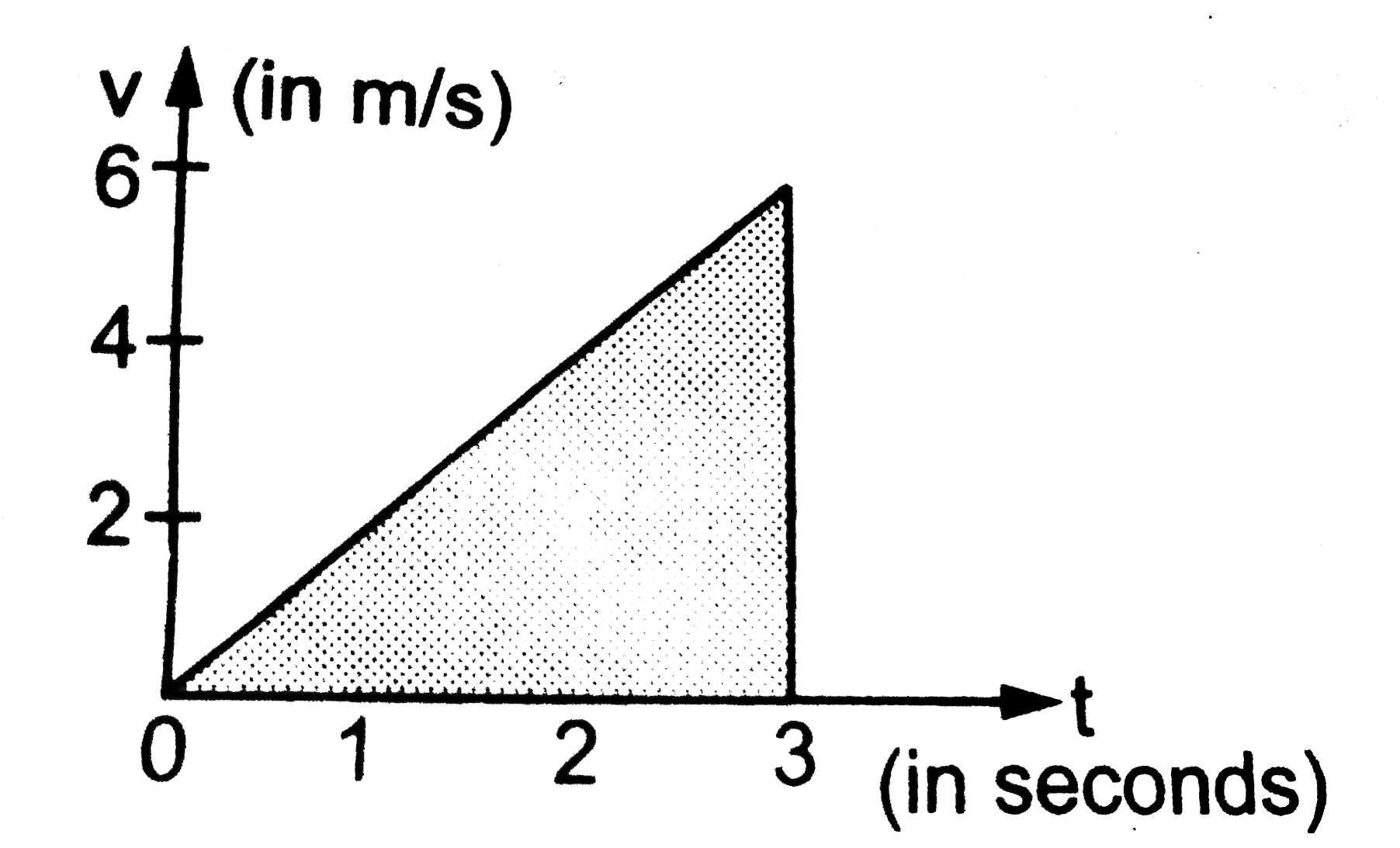A9mB5mC2mD1m
The velocity of a particle varies with time as per the figure shown. The distance travelled by the particle in 10 seconds is ?(m/s)
View SolutionA particle starting from rest moves in a straight line with acceleration as shown in the a-t graph. Find the distance (in m) travelled by the particle in the first four seconds from start of its motion.
Q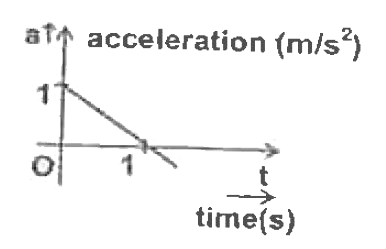
View SolutionA particle is moving in a straight line under acceleration a=54−18t. The particle starts from the origin.
(a) Sketch the a-t, v-t and s-t graph.
(b) Find the distance traveled in the first 9 s. (Acceleration is in m/s2, time is in second)View SolutionThe position x of a particle varies with time t as x=6+12t−2t2 where x is in metre and t is in seconds. The distance travelled by the particle in first five seconds is
View SolutionThe variation of velocity of a particle with time moving along a straight line is illustrated in the following figure. The distance travelled by the particle in four seconds is.
View Solution