Three insects A,B and C are situated at the vertices of an equillateral triangle of side 1. the insect A heads towards B,B towards C,C towards A with constant speeds v such that they always remain at the vertices of an equilateral triangle. Find the (a) time of their meeting (b) equation of path traced by one insect relative to the other.

Video Solution

Text Solution

Verified by Experts

After a time t, let the distance of spearation between the insects be r. the velocity of approach (component of relative velocity $u_{r e l} = v + v {cos 60}^{\circ} = \frac{3 v}{2}$

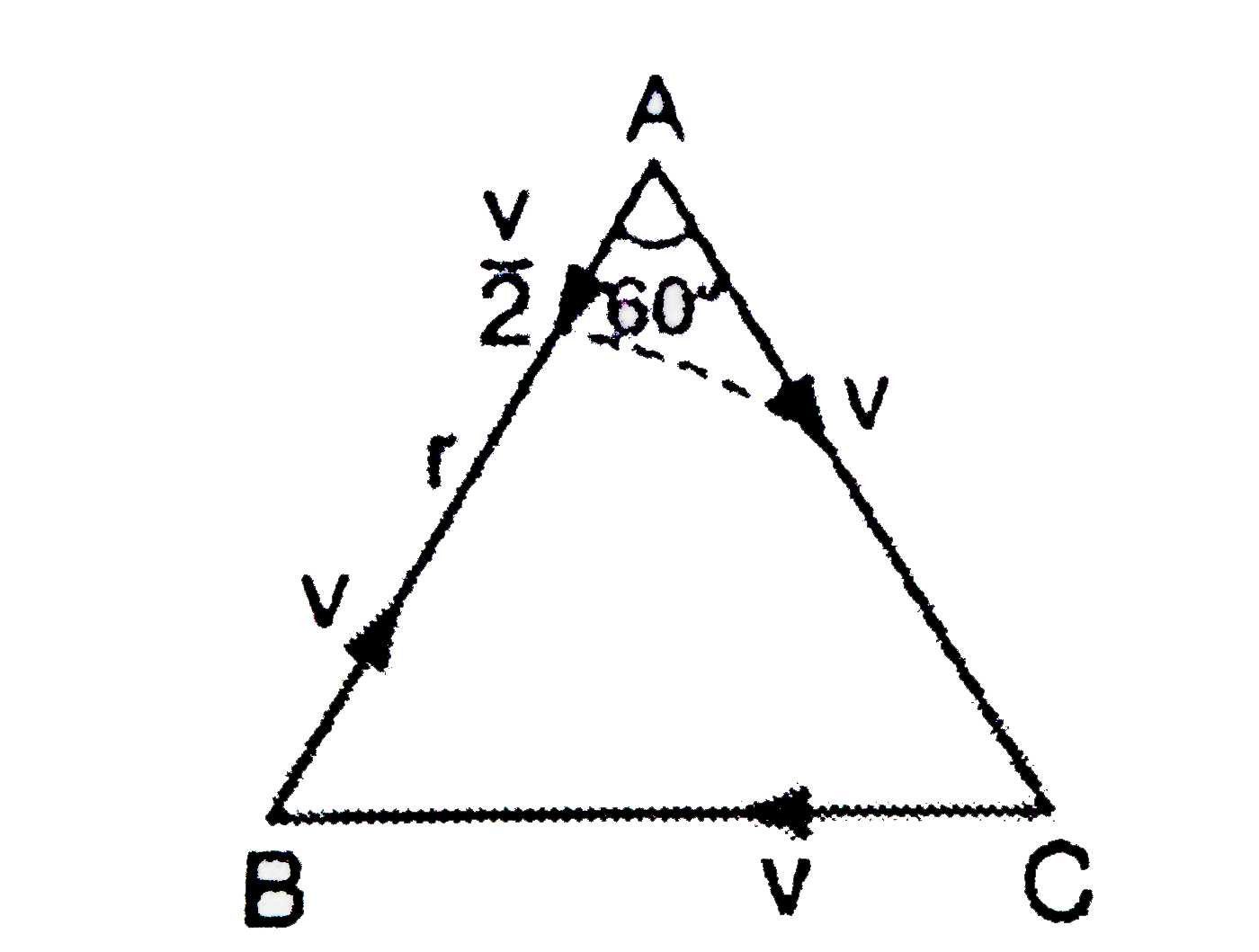
Since, ${(v_{r e l})}_{∣ ∣} d t = - d r$ , submitting ${(v_{R e l})}_{∣ ∣} = \frac{3 v}{2}$ , we obtain
$\frac{3 v}{2} d t = - d r$ ......(i)
As , $r = l at t = 0$ and $r = 0 at t = τ$ (time of meeting ), integrating both sides, we have
$\frac{3 v}{2} \int_{0}^{τ} d t = - \int_{l}^{0} d r$
This gives, $τ = \frac{2 l}{3 v}$

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
Three particles $A, B$ and $C$ and situated at the vertices of an equilateral triangle $A B C$ of side of length $l$ at time $t = 0$ ,Each of the particles move with constant speed $u$ . A always has its velocity along $A B, B$ along $B C$ and $C$ along $C A$ .

AThe time after which they meet is $\frac{2 l}{3 u}$
BTotal distance travelled by each particle before they meet is $\frac{2 l}{3}$
CAverage velocity during the motion is $\frac{\sqrt{3} u}{2}$
DRelative velocity of apporach between any two particles is $\frac{3 u}{2}$
Question 2 - Select One
Three particles A, B and C are situated at the vertices of an equilateral triangle ABC of side d at time $t = 0 .$ Each of the particles moves with constant speed v. A always has its velocity along AB, B along BC and C along CA. At what time will the particles meet each other?
A $t = \frac{d}{v}$
B $t = \frac{3 d}{2 v}$
C $t = \frac{2 d}{3 v}$
D $t = 0$
Question 3 - Select One
IF $\to a, \to b, \to c$ are the position vectors of the vertices of an equilateral triangle whose orthocentre is at the origin, then
A $a + b + c = 0$
B $a^{2} = b^{2} + c^{2}$
C $a + b = c$
Dnone of these

GRB PUBLICATION-MOTION IN TWO AND THREE DIMENSIONS-All Questions

Home
Ask Doubt
Profile