Two particles are projected simu ltaneously from points A and B respectively and they move in same plane. Find.
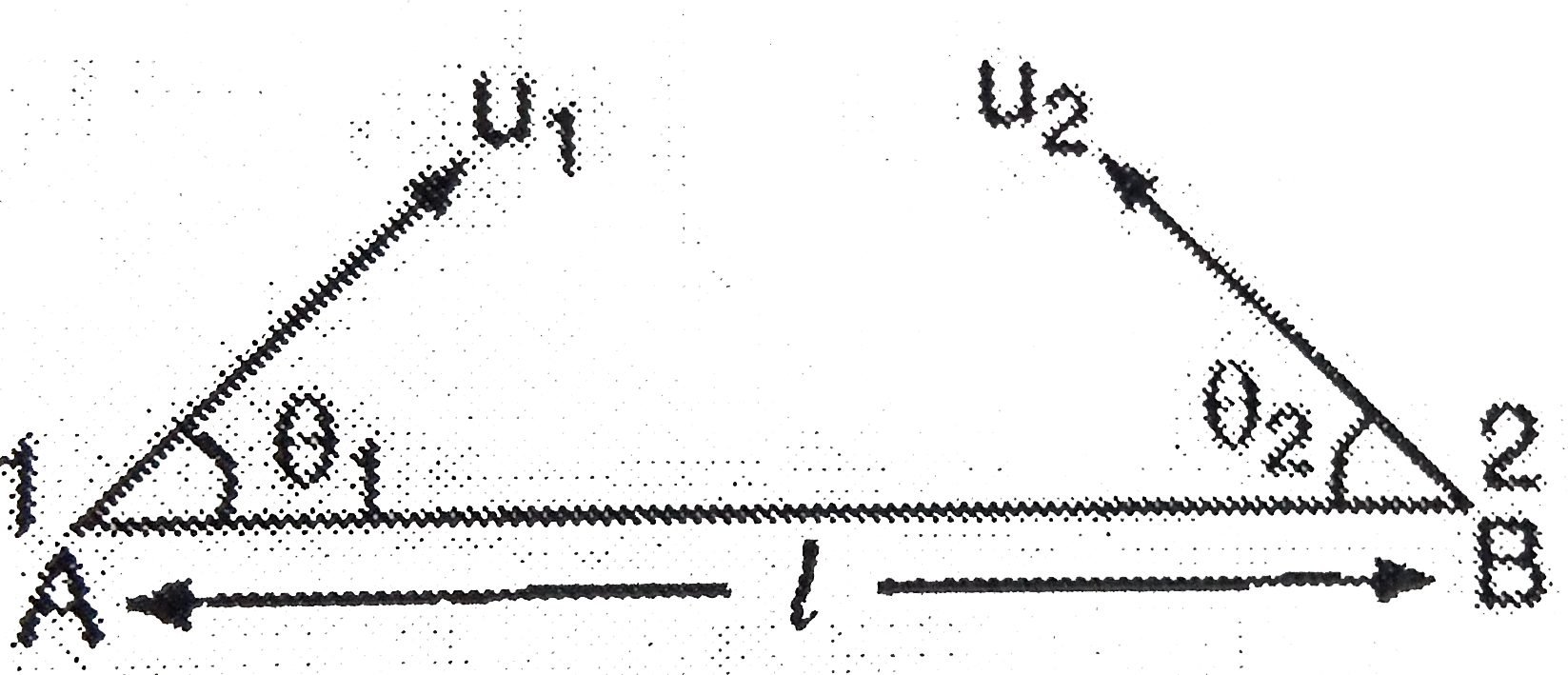
(a) the separation when they are closest to each other.
(b) the time elapsed to come closest to each other.
(c) condition that they collide in air.
(d) initial velocity of approch between the particles.
(e) initial angu lar velocity of first particle w.r.t. second particle.
Velocity of 1st particle at any instant 't'
→v1=u1cosθ1ˆi+(u2sinθ2−>)ˆj ........(i)
Velocity of 2nd particle at the same instant 't'
→v2=u2cosθ2(−ˆi)+(u2sinθ2−>)ˆj...... (ii)
∴velocity of 1st particle w.r.t. 2nd particle
→v12=→v1−→v2=(u1cosθ1+u2cosθ2)ˆi
+(u1sinθ1−u2sintehta2)ˆj .........(iii)
tanϕ=u1sinθ1−u2sinθ∘u1cosθ1+u2cosθ2 .........(iv)
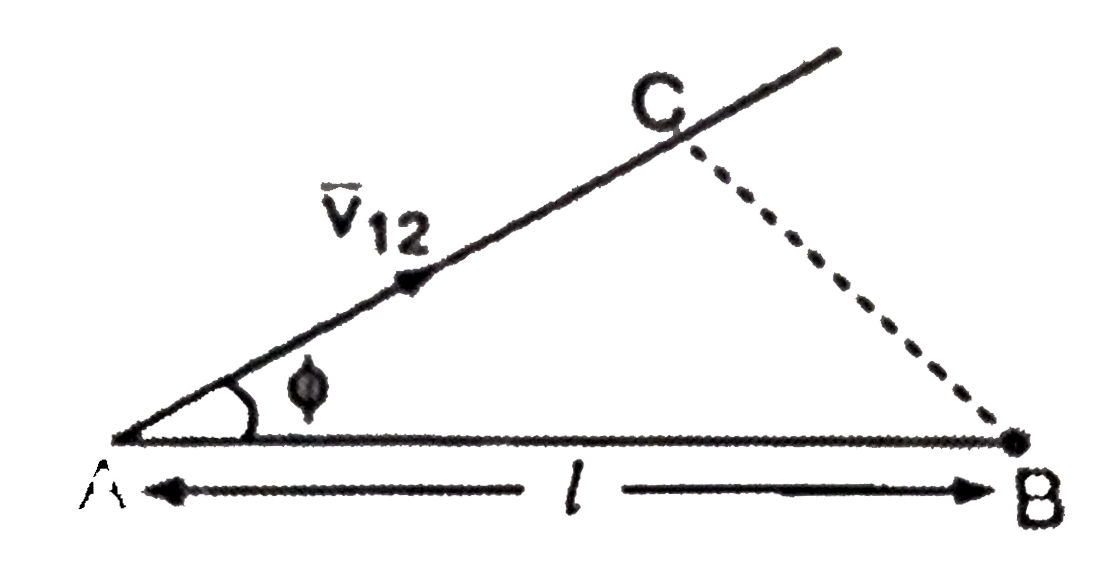
(a) Separation when they are closest is BV=lsinϕ
(b) t=AC|→v12|=lcosϕ|→v12|
|→v12|=√(u1cosθ1+u2cosθ2)2+(u1sinθ1−u2sinθ2)2
(c) If they collide then BC (minimum speration)=0
i.e., ϕ=0
∴tanϕ=0
⇒u1sinθ1=u∘sinθ2 from equation (iv)
(d) Velocity of approach
=u1cosθ1+u2cosθ2
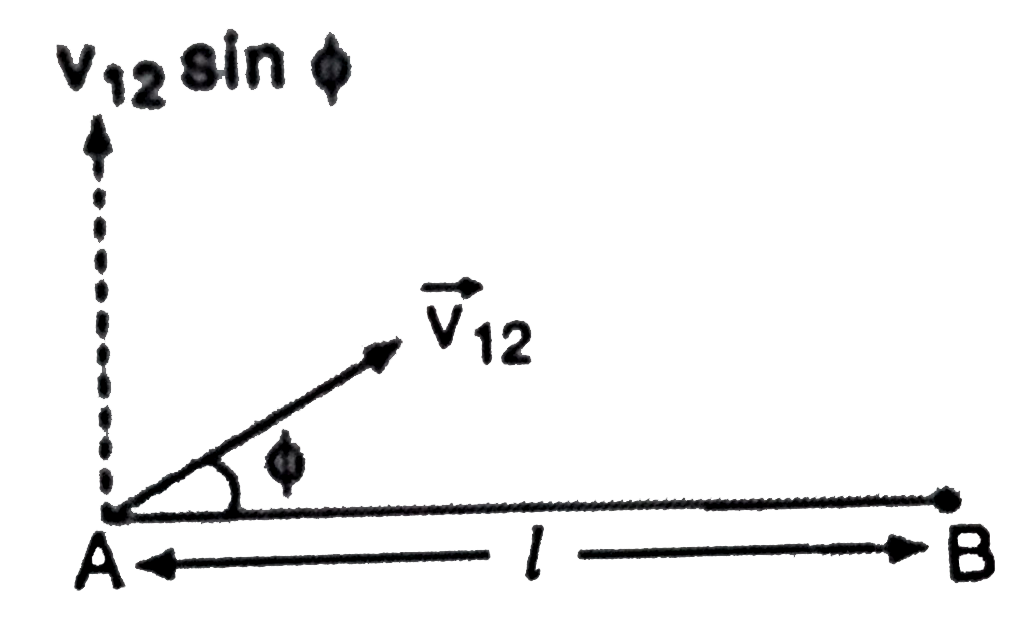
(e) ω12=ωAB=v12sinϕl
ω12=u1sinθ1−u2sinθ2l
Topper's Solved these Questions
Similar Questions
A particle moves in a straight line with a uniform acceleration a. Initial velocity of the particle is zero. Find the average velocity of the particle in first 's' distance.
View SolutionTwo particles were projected simu ltaneously in horizontal plane with same velocity u perpendicu lar to each other. The time after which their velocities makes angle 60∘ with each other is kug. Find the value of k
View Solution
Knowledge Check
Two particles starting from a point on a circle of radius 4m in horizontal plane move along the respectively in opposite directions. The particle will collide with each other after a time of
A3.0sB2.5sC2.0sD1.5sTwo particle are projected with same initial velocities at an angle 30∘ and 60∘ with the horizontal .Then
Atheir heights will be equalBtheir height will be differentCtheir range of flight will be equalDtheir ranges will be differentTwo identical particles move towards each other with velocity 2v and v respectively. The velocity of centre of mass is
AVBV/3CV/2DZero
Particles AandB move with constant and equal speeds in a circle as shown in (Fig. 5.164). Find the angular velocity of the particle A with respect to B, if the angular velocity of particle Aw.r.t.O is ω.
 .
.
View SolutionA particle move so that its position verctor varies with time as →r=Acosωtˆi+Asinωtˆj. Find the
a. initial velocity of the particle,
b. angle between the position vector and velocity of the particle at any time, and
c. speed at any instant.
View SolutionTwo particles are simultaneously projected in the same vertical plane from the same point with velocities u and v at angles αandβ with horizontal. Find the time that elapses when their velocities are parallel.
View SolutionTwo identical particles move towards each other with velocity 2v and v respectively. The velocity of centre of mass is
View SolutionA particle is projected from the mid-point of the line joining two fixed particles each of mass m. If the separation between the fixed particles is l, the minimum velocity of projection of the particle so as to escape is equal to
View Solution
