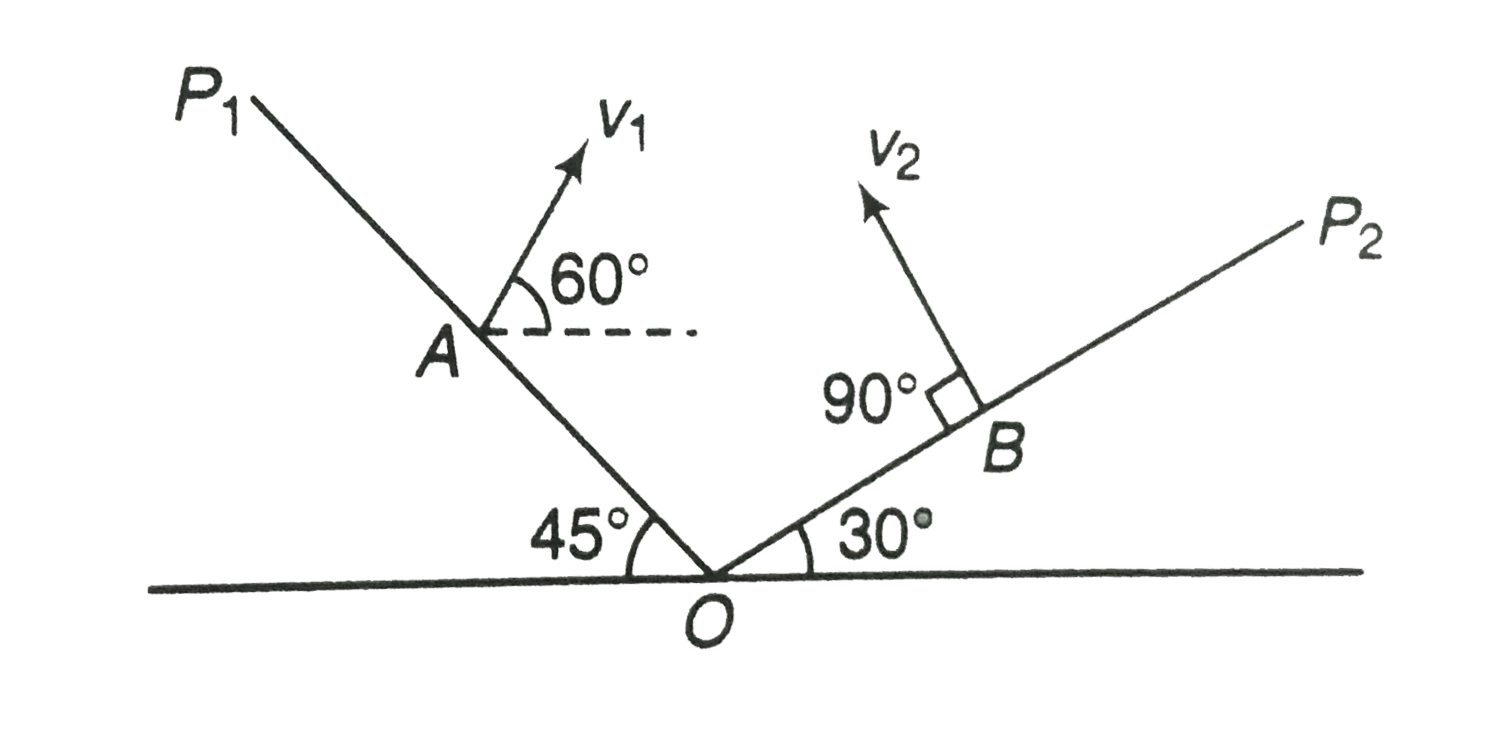
A particle is projected from an inclined plane OP1 from A with velocity v1=8ms−1 at an angle 60∘ with horizontal. An another particle is projected at the same instant from B with velocity v2=16ms−1 and perpendicular to the plane OP2 as shown in figure. After time 10(√3) s there separation was minimum and found to be 70m. Then find distance AB.
250m
500m
750m
1000m
The correct Answer is:a
(vB.A)horizontal=v2cos60+v1cos60=12m/s.
(VB.A.)vertical=v2sin60−v1sin60=4√3m/s
vB.A.=√(12)2+(4√32)=√192
x=v21t=√192×10√3=240m
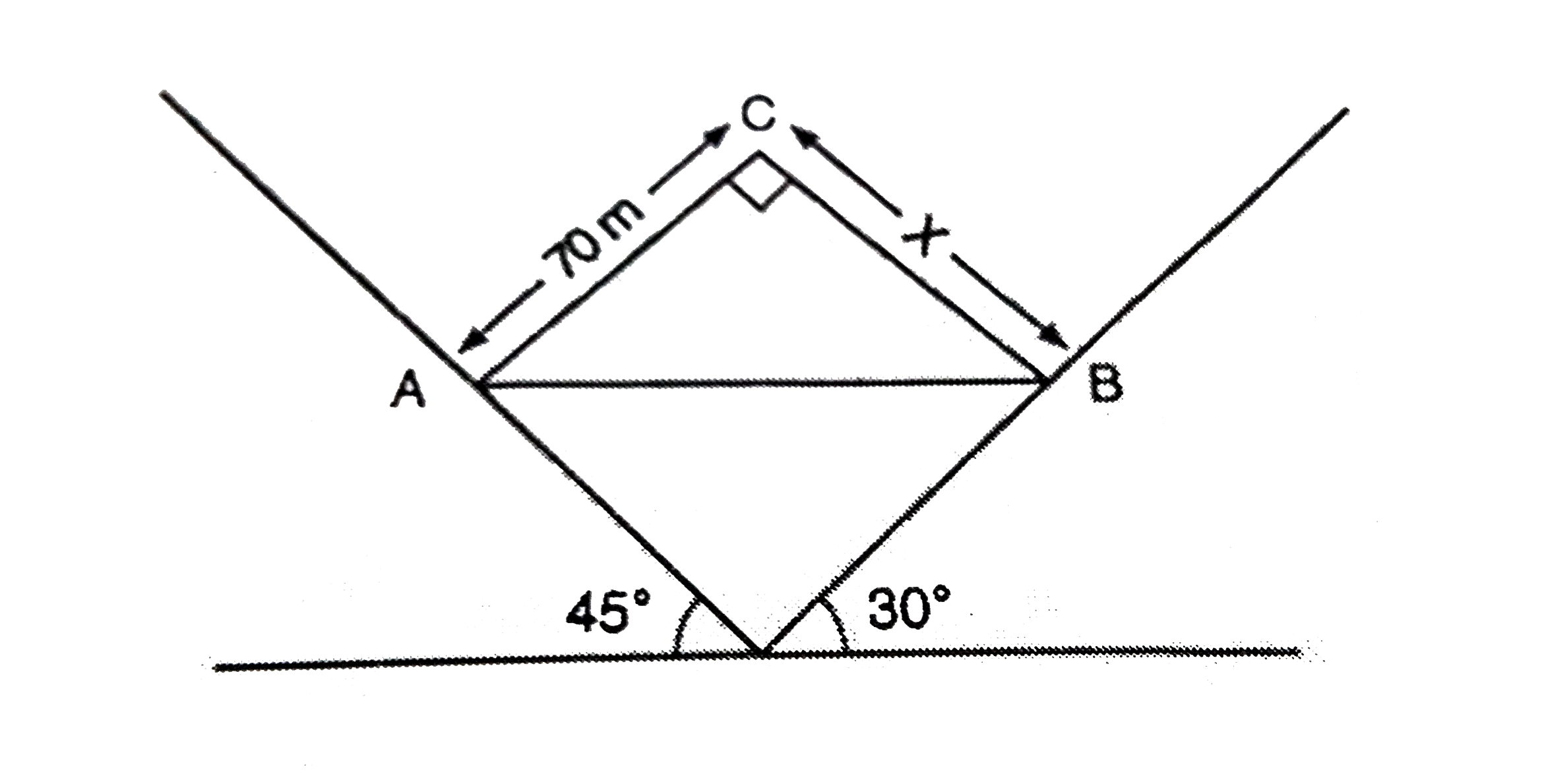
From ΔABC
AB2=AC2+BC2
AB=250m
Topper's Solved these Questions
Similar Questions
A particle is projected from the bottom of an inclined plane of inclination 30∘ with velocity of 40m/s at an angle of 60∘ with horizontal. Find the speed of the particle when its velocity vector is parallel to the plane. Take g=10m/s2.
View SolutionA particle is projected with a velocity 10 m//s at an angle 37∘ to the horizontal. Find the location at which the particle is at a height 1 m from point of projection.
View Solution
Knowledge Check
- Question 1 - Select One
A ball is projected from point A with velocity 10ms−1 perpendicular to the inclined plane as shown in figure. Range of the ball on the inclined plane is
 A403mB203mC123mD603m
A403mB203mC123mD603m - Question 2 - Select One
A ball is projected from point A with velocity 10ms−1 perpendicular to the inclined plane as shown in figure. Range of the ball on the inclined plane is
 A403mB2013mC1320mD1340m
A403mB2013mC1320mD1340m - Question 3 - Select One or More
A particle is projected at an angle θ=30∘ with the horizontal, with a velocity of 10ms−1. Then
AAfter 2 s, the velocity of particle makes an angle of 60∘ with initial velocity vector.BAfter 1 s, the velocity of particles makes an angle of 60∘ with initial velocity vector.CThe magnitude of velocity of particle after 1 s is 10ms−1.DThe magnitude of velocity of particle after 1 s is 5ms−1.
A particle is projected with a velocity of 20ms−1 at an angle of 60∘ to the horizontal. The particle hits the horizontal plane again during its journey. What will be the time of impact ?
View SolutionA particle is projected with velocity 20ms−1 at angle 60∘ with horizontal . The radius of curvature of trajectory , at the instant when velocity of projectile become perpendicular to velocity of projection is , (g=10ms−1)
View SolutionA particle is projected from a horizontal plane with a velocity of 8√2ms−1 ms at an angle θ. At highest point its velocity is found to be 8ms−1 Its range will be (g=10ms−2)
View SolutionA particle is projected from horizontal ground with speed 5ms−1 at 53∘ with horizontal. Find time after which velocity of particle will be 45∘ with horizontal:
View SolutionA particle is projected with velocity 50 m/s at an angle 60∘ with the horizontal from the ground. The time after which its velocity will make an angle 45∘ with the horizontal is
View Solution

