Two blocks each of mass M are resting on a frictionless inclined plane as shown in fig then:

the block A moves down the plane
the block B moves down the plane
both the blocks remain at rest
both the blocks move down the plane
The correct Answer is:A
The force acting down the plane for blocks A and B are:
Since the block A moves down the plane.
Topper's Solved these Questions
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - More than one choice is correct
15 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Assertion- Reason
4 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Problem for practice
30 Videos
- BASIC MATHEMATICSBOOK - GRB PUBLICATIONCHAPTER - BASIC MATHEMATICSEXERCISE - Problems For Practice
35 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type
11 Videos
Similar Questions
A block of mas M is resting on an inclined plane as shown in the figure. The inclination of the plane to the horizontal is gradually increased. It is found that when the angle of inclination is θ the block just begins to slide down the plane. What is the minimum force F applied parallel to the plane that would just make the block move up the plane ?
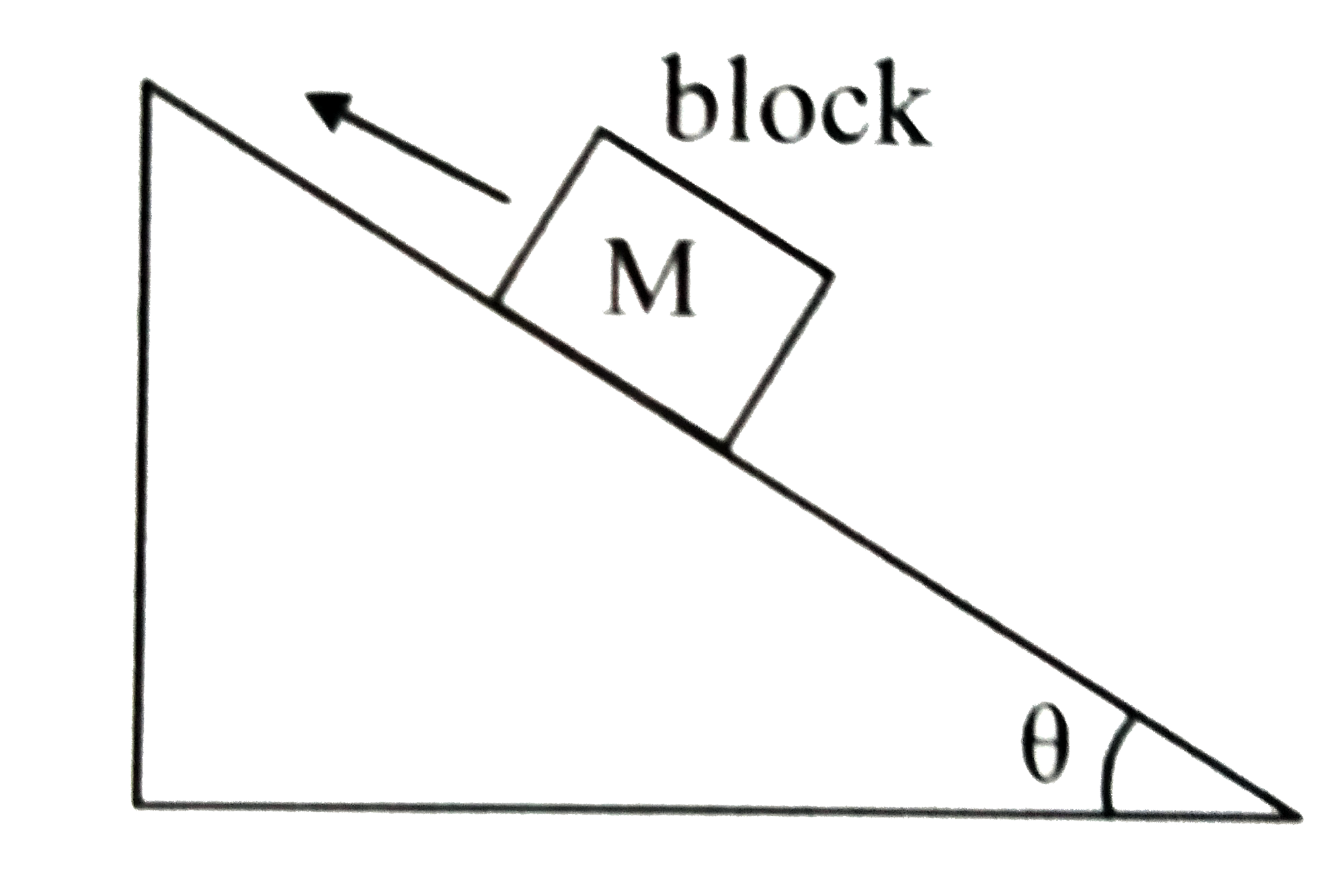
View SolutionA block of mas M is resting on an inclined plane as shown in the figure. The inclination of the plane to the horizontal is gradually increased. It is found that when the angle of inclination is θ the block just begins to slide down the plane. What is the minimum force F applied parallel to the plane that would just make the block move up the plane ?

View Solution
Knowledge Check
Block A of mass 35 kg is resting on a frictionless floor.
 A0.8ms−2B2.4ms−2C0.4ms−2D4.4ms−2
A0.8ms−2B2.4ms−2C0.4ms−2D4.4ms−2A small block of mass M moves on a frictionless surface of an inclined plane, as shown in the figure. The angle of the incline suddenly changes from 60∘ to 30∘ at point B. The block is many at rest at A. Assume that collisions between the block id the incline are totally inelastic.
The speed of the block at point C, immediately before it leaves the second incline
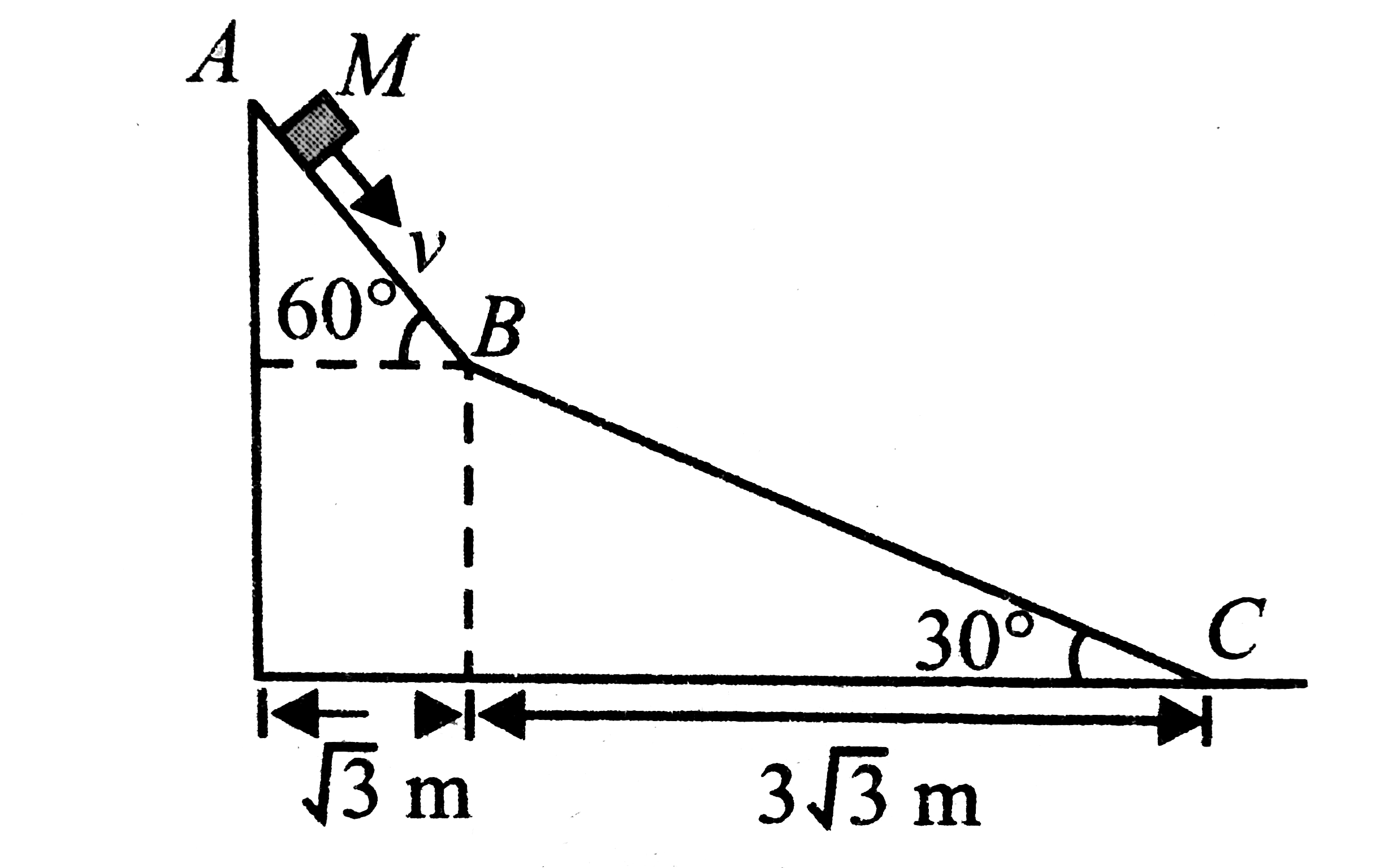 A√120m/sB√105m/sC√90m/sD√75m/s
A√120m/sB√105m/sC√90m/sD√75m/sTwo blocks, each having a mass M, rest on frictionless surfaces as shown in the figure. If the pulleys are light and frictionless and M on the incline is allowed to move down, then the tension in string will be
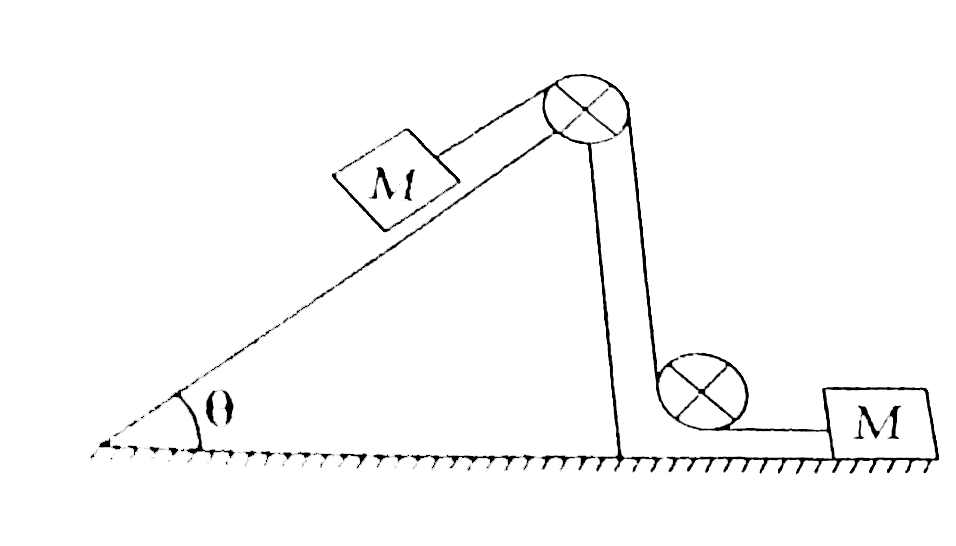 A23MgsinθB32MgsinθCMgsinθ2D2Mgsinθ
A23MgsinθB32MgsinθCMgsinθ2D2Mgsinθ
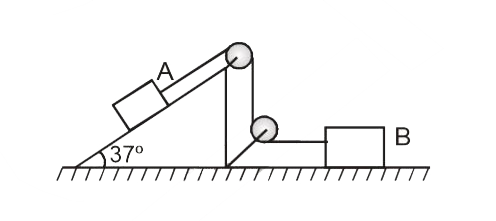
Two blocks A and B each having a mass of 20kg, rest on frictionless surfaces as shown in the figure below.Assuming the puelleys to be light and frictionless, compute :
(a) the time required for block A, to move down by 2m on the plane, starting from rest,
( b) tension in the string, connecting the blocks.
View SolutionA block of mass m can slide along a frictionless inclined plane, is attached to a ideal spring of spring constant as shown in the figure. Find the period of its oscillation. (Frame of reference attached to the wedge is at rest)
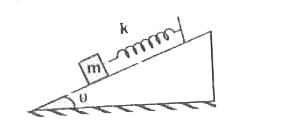
View SolutionTwo blocks 4 kg and 2 kg are sliding down an incline plane as shown in fig The acceleration of 2 kg block is:

View SolutionA block of mass 'm' is released on the top of a frictionless incline as shown in the figure. The time period of the oscillation of the block is

View SolutionA block of mass 3kg is at rest on a rough inclined plane as shown in the figure. The magnitude of net force exerted by the surface on the block will be

View Solution
