Two masses m1 and m2 are connected to the ends of a massless string that passes over a pulley fixed at the top of a double incline as shown. Assuming m1>m2 acceleration of the system is:

m1gsinθ1+m2gsinθ2m1+m2
m1gsinθ1−m2gsinθ2m1−m2
m1gsinθ1−m2gsinθ2m1+m2
(m1+m2)(sinθ1+sinθ2)gm1−m2
The correct Answer is:C
m1gsinθ1−T=m1a
T−m2gsinθ2=m2a
By solving this, we get acceleration.
Topper's Solved these Questions
- BOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - More than one choice is correct15videos
FORCE AND NEWTONS LAWS OF MOTION
- BOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Assertion- Reason4videos
FORCE AND NEWTONS LAWS OF MOTION
- BOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Problem for practice30videos
FORCE AND NEWTONS LAWS OF MOTION
- BOOK - GRB PUBLICATIONCHAPTER - BASIC MATHEMATICSEXERCISE - Problems For Practice35videos
BASIC MATHEMATICS
- BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type11videos
FRICTION AND CIRCULAR MOTION
Similar Questions
Two masses M1 and M2 are attached to the ends of a light string which passes over a massless pulley attached to the top of a double inclined smooth plane of angles of inclination α and β.The tension in the string is :
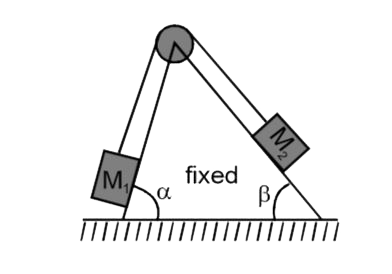 View Solution
View SolutionTwo masses M1 and M2 are attached to the ends of a string which passes over a pulley attached to the top of an inclined plane. The angle of inclination of the plane is 30∘ and M1=10kg,M2=5kg. What is the acceleration of mass M2 ?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two masses 2 kg and 3 kg are attached to the end of the string passed over a pulley fixed at the top. The tension and acceleration are
A7g8,g8B21g8,g8C21g8,g5D12g5,g5 - Question 2 - Select One
Two masses m1 and m2 are attached to the ends of a massless string which passes over a frictionless pulley attached to the top of an inclined plane. The angle of inclination of the plane is θ. Take g=10ms−2
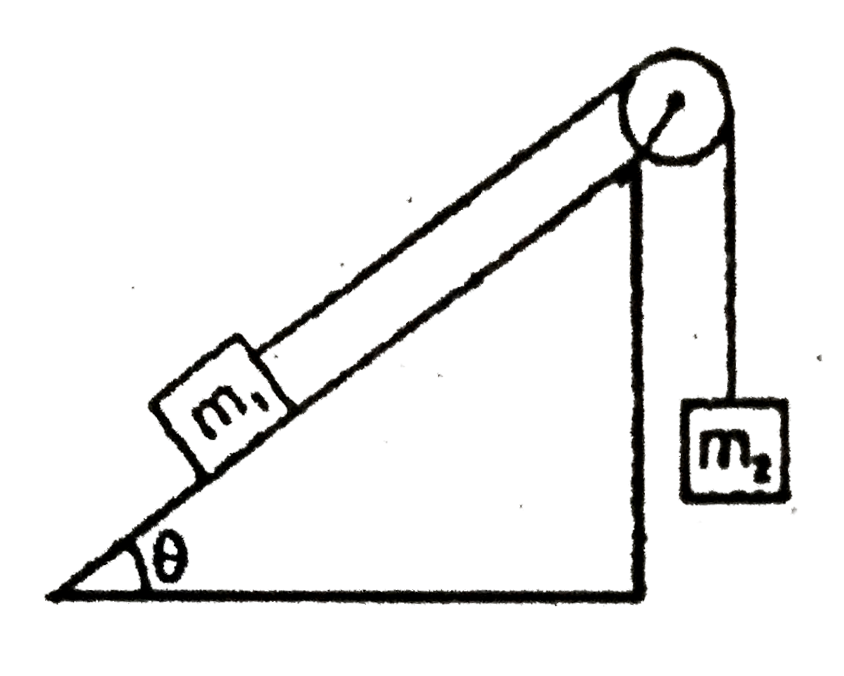
if m1=10kg,m2=5kg,θ=30∘, what is the acceleration of mass m2?AzeroB(2/3)ms−2C5ms−2D10/3ms−2 - Question 3 - Select One
Two masses M1andM2 are attached to the ends of string which passes over the pulley attached to the top of a double inclined plane. The angles of inclination of the inclined planes are αandβ. Take g=10ms−2. If M1=M2 and α=β, what is the acceleration of the system?
AzeroB2.5m/s−2C5m/s−2D10m/s−2
Two masses m1andm2 are connected to the end of a string passing over a smooth pulley . The magnitude of tension in the string is T and the masses are moving with magnitude of acceleration a . If the masses are interchanged , then
View SolutionTwo blocks of masses m1 and m2 are connected by a string of negligible mass which pass over a frictionless pulley fixed on the top of an inclined plane as shown in figure. The coefficient of friction between m1 and plane is μ.
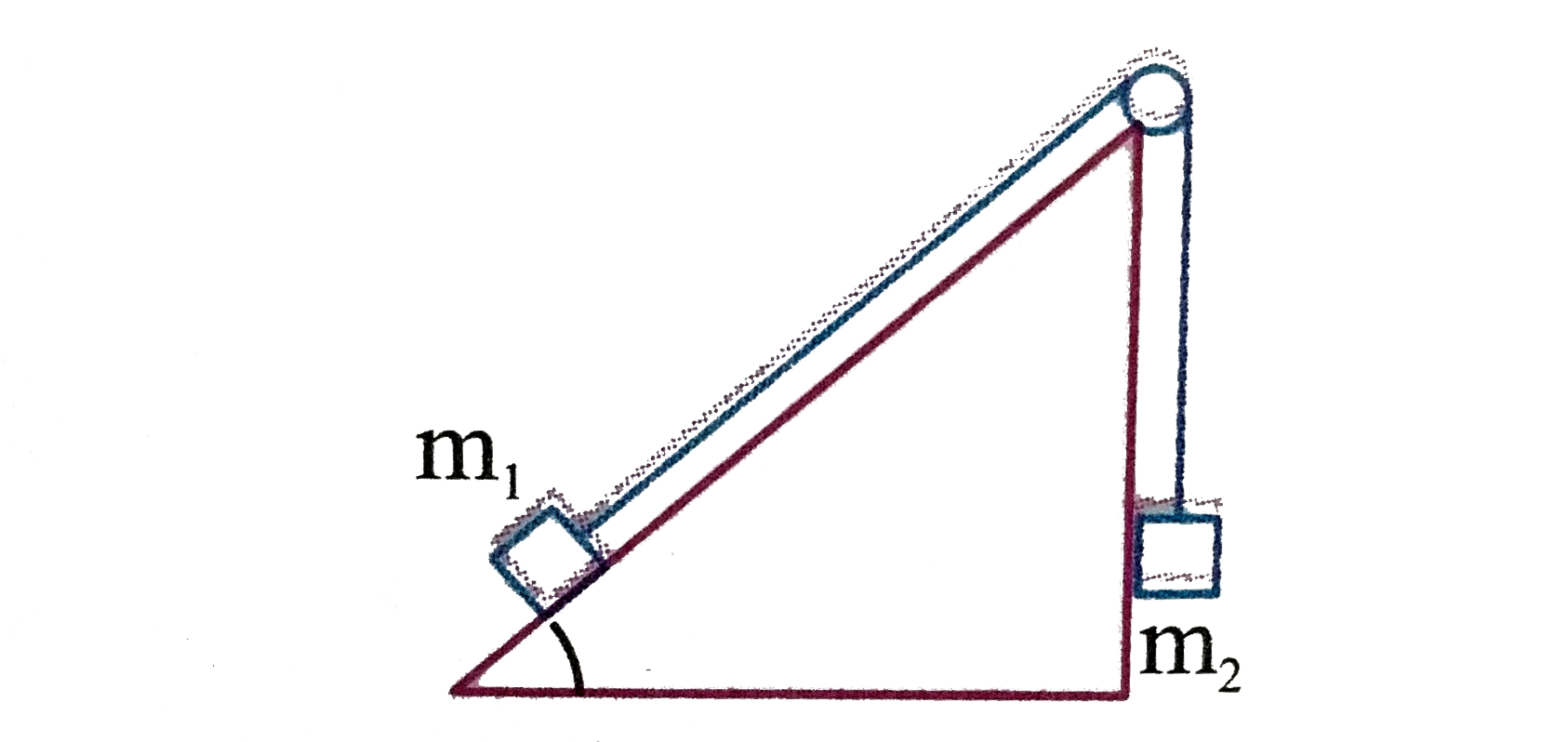 View Solution
View SolutionTwo masses M1=5kg,M2=10kg are connected at the ends of an inextensible string passing over a frictionless pulley as shown. When masses are released, then acceleration of masses will be
 View Solution
View SolutionTwo masses m1=4kgandm2=2kg are connected with an nextansible , massless string that passes over a frictionless pulley and through a slit as, shown the string is vertical upon by a conatant friction force 10 N by the slit as it moves (use g=10m/s2
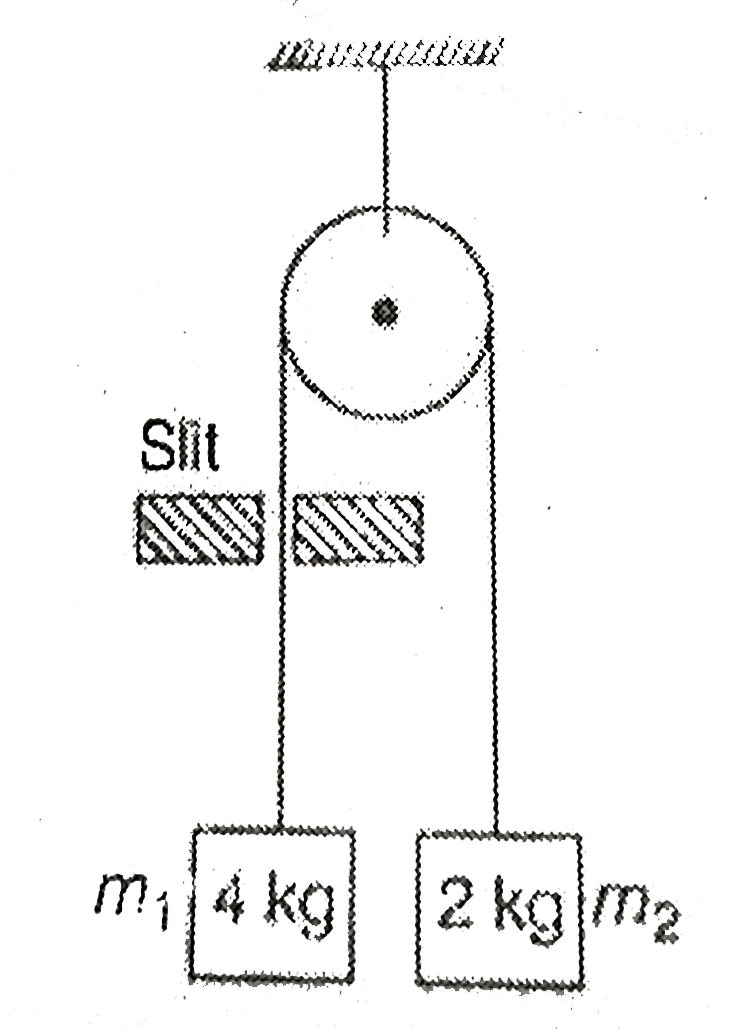 View Solution
View SolutionTwo bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
View Solution

