A man wishes to estimate the distance of a nearby tower from him. He stands at a point A in front of the tower C and spots a very distant object O in line with AC. He then walks perpendicualr to AC upto B, a distaance of 100m and looks at O and C again. Since O is very distant, the direction of BO is practically the same as AO, but he finds the line of sight of C shifted from the original line of sight by an angle θ=40∘(θis known as parallax). Estimate the distance fo the tower C from his original position A.
We have, parallax angle θ=40∘
From Fig. 2.3 AB=ACtanθ
AC=AB/tanθ=100m/tan40∘
=100m/0.8391=119m
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - UNITS AND MEASUREMENTEXERCISE - EXERCISE33videos
UNITS AND MEASUREMENT
- BOOK - NCERTCHAPTER - UNITS AND MEASUREMENTEXERCISE - QUESTION1videos
UNITS AND MEASUREMENT
- BOOK - NCERTCHAPTER - THERMODYNAMICSEXERCISE - EXERCISE10videos
THERMODYNAMICS
- BOOK - NCERTCHAPTER - WAVESEXERCISE - EXERCISE27videos
WAVES
Similar Questions
The angles of elevation of the top of an inaccessible tower from two points on the same straight line from the base of the tower are 30° and 60° respectively. If the points are separated at a distance of 100 m, then the height of the tower is close to :
View SolutionThe angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6m.
View Solution
Knowledge Check
- Question 1 - Select One
The angle of elevation of the top of a tower from the point P and Q at distance of a and b respectively from the base of the tower and in the same straight line with it are complementary .The height of the tower is
A√abBabCabDa2b2 - Question 2 - Select One
A person stands at a point A due south of a tower and observes that its elevation is 60∘. He then walks westwards towards B, where the elevation is 45∘. At a point C on AB produced, he finds it to be 30∘. Then AB/BC is equal to
A1/2B1C2D5/2 - Question 3 - Select One
The angles of elevation of e top of an inaccessible tower from two points on the same straight line from the base of the tower are 30∘and60∘, respectively. If the points are separated at a distance of 100 m, then the height of the tower is close to
A86.5mB80.6mC82.6mD80.6m
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
View SolutionIn the figure-2, the angle of elevation of the top of tower AC from a point B on the ground is 60∘ . If the height of the tower is 20 m. find the distance of the point from the foot of the tower.
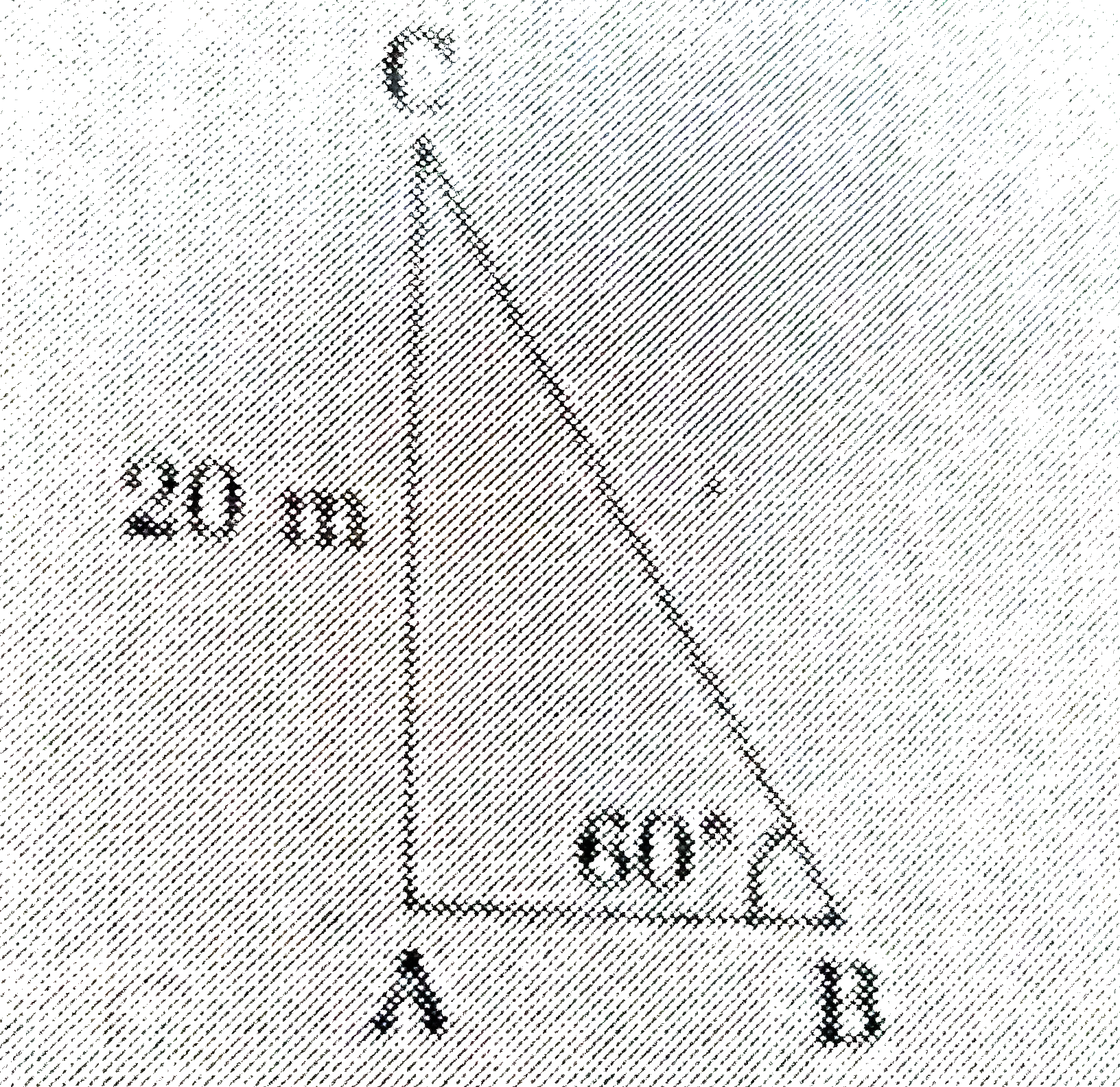 View Solution
View SolutionThe angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30∘. Find the height of the tower.
View SolutionA tower of height h stands at a point O on the ground. Two poles of height a and b stand at the points A and B respectively such that O lies on the line joining A and B. If the angle of elevation of the top of the tower at the foot of one pole is ame as at the top of the other pole, then h is equal to
View SolutionA man is standing on the top of building of height 5 m. If he subtends equal angles at a point on the ground distant 13 m from the base of the building then the height of the man is
View Solution

